Using renormalization group methods to study how the brain processes information

Past neuroscience research suggests that biological neural networks in the brain could self-organize into a critical state. In physics, a critical state is essentially a point that marks the transition between ordered and disordered phases of matter.

Researchers at the Jülich Research Centre, RWTH Aachen University, and Sorbonne Université have recently introduced a theory that could help to explain criticality in the brain. This theory, introduced in a paper published in Physical Review Letters, is based on a prototypical neural field theory, known as the "stochastic Wilson-Cowan equation."

"Previous works have provided evidence that the brain operates at a critical point," Lorenzo Tiberi, Jonas Stapmanns, Tobias Kühn, Thomas Luu, David Dahmen, and Moritz Helias, the researchers who carried out the study, told Phys.org, via email. "Yet, it is unclear which of the many possible types of criticalities is specifically implemented by the brain, and how the latter may exploit criticality for optimal computation."

To classify the different types of criticality physicists typically use methods within the so-called renormalization group (RG). These are essentially formal approaches that can be used to systematically investigate changes in a physical system at different scales.

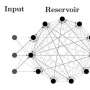
In their study, the researchers adapted these traditional methods and integrated them with a prototypical neuronal field model first proposed by Wilson and Cowan. They then specifically applied them to the field of neuroscience to examine criticality in biological neural networks.

"In our work, we study the well-established Wilson-Cowan equations with stochastic input, so the model we use is not new," Tiberi, Stapmanns and their colleagues said. "However, using RG techniques, we arrive at an original result."

To complete computational tasks, cognitive tasks that involve calculations, the human brain needs to be able to memorize the input data it receives and then combine it in complex ways. This in turn allows it to process the information and solve the computational problem.

"We discovered that criticality in the Wilson-Cowan neural field model is of the Gell-Mann-Low type, which, among all types of criticality, specifically offers an optimal balance between memorizing input data and combining it in complex ways," Tiberi, Stapmanns, and their colleagues said.

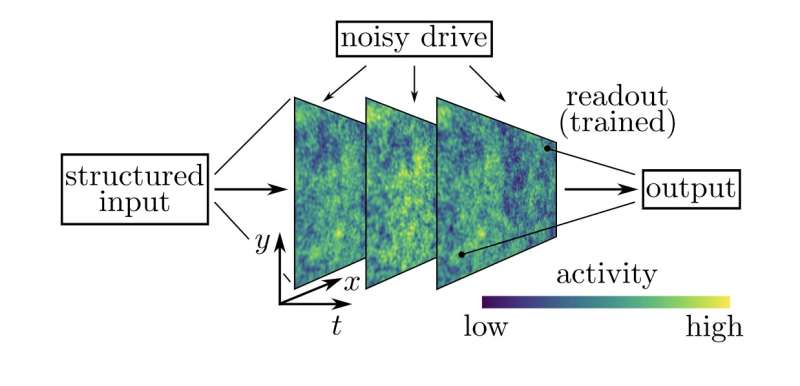
Using RG methods, the researchers managed to study the effects of nonlinear interactions in the Wilson-Cowan model, which are crucial to understanding how the brain processes information. This is a remarkable achievement, as the mean-field methods used by other teams in the past were unable to capture these effects, particularly when interactions are strong enough to shape brain dynamics on a macroscopic scale.

"We expect that RG methods will be of use to study other non-linear processes in neuronal networks," the team explained. "Moreover, we draw connections to other areas of physics: The concept of Gell-Man-Low criticality originates from quantum field theory and the Kardar-Parisi-Zhang model, which closely relates to our model, has originally been used to describe dynamic growth of interfaces."

In the future, the theory introduced by this team of researchers could be used to examine various other brain dynamics and neural processes, reaching beyond criticality. In addition, it could ultimately pave the way toward the introduction of other theoretical constructs merging physics and neuroscience.

"In the brain, the strength of connections between neurons is highly variable to an extent that in a first approximation it can be described as random," the researchers added. "We now plan to apply our methods to neural models that include this feature and see what effect this has, if any, on the type of criticality we find."

© 2022 Science X Network