Algorithm to increase the efficiency of quantum computers
Quantum computers have the potential to solve important problems that are beyond reach even for the most powerful supercomputers, but they require an entirely new way of programming and creating algorithms.
Universities and major tech companies are spearheading research on how to develop these new algorithms. In a recent collaboration between University of Helsinki, Aalto University, University of Turku, and IBM Research Europe-Zurich, a team of researchers have developed a new method to speed up calculations on quantum computers. The results are published in the journal PRX Quantum of the American Physical Society.
"Unlike classical computers, which use bits to store ones and zeros, information is stored in the qubits of a quantum processor in the form of a quantum state, or a wavefunction," says postdoctoral researcher Guillermo García-Pérez from the Department of Physics at the University of Helsinki, first author of the paper.
Special procedures are thus required to read out data from quantum computers. Quantum algorithms also require a set of inputs, provided for example as real numbers, and a list of operations to be performed on some reference initial state.
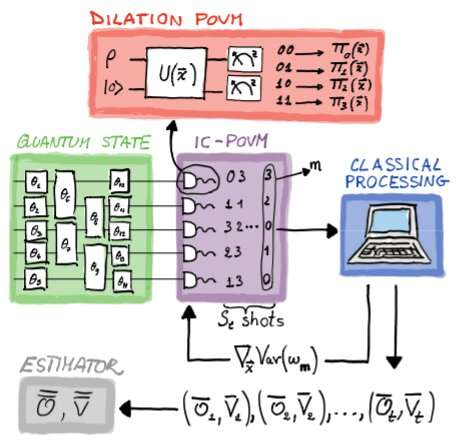
"The quantum state used is, in fact, generally impossible to reconstruct on conventional computers, so useful insights must be extracted by performing specific observations (which quantum physicists refer to as measurements)," says García-Pérez.
The problem with this is the large number of measurements required for many popular applications of quantum computers (like the so-called Variational Quantum Eigensolver, which can be used to overcome important limitations in the study of chemistry, for instance in drug discovery). The number of calculations required is known to grow very quickly with the size of the system one wants to simulate, even if only partial information is needed. This makes the process hard to scale up, slowing down the computation and consuming a lot of computational resources.
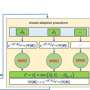
The method proposed by García-Pérez and co-authors uses a generalized class of quantum measurements that are adapted throughout the calculation in order to extract the information stored in the quantum state efficiently. This drastically reduces the number of iterations, and therefore the time and computational cost, needed to obtain high-precision simulations.
The method can reuse previous measurement outcomes and adjust its own settings. Subsequent runs are increasingly accurate, and the collected data can be reused again and again to calculate other properties of the system without additional costs.
"We make the most out of every sample by combining all data produced. At the same time, we fine-tune the measurement to produce highly accurate estimates of the quantity under study, such as the energy of a molecule of interest. Putting these ingredients together, we can decrease the expected runtime by several orders of magnitude," says García-Pérez.
More information: Guillermo García-Pérez et al, Learning to Measure: Adaptive Informationally Complete Generalized Measurements for Quantum Algorithms, PRX Quantum (2021). DOI: 10.1103/PRXQuantum.2.040342
Provided by University of Helsinki