Mathematical model offers new insights into spread of epidemics
Mathematical models have been widely used to guide government decisions on the COVID-19 pandemic, from forecasting outcomes to even testing potential interventions.
However, the complexity of real-world scenarios still poses new theoretical challenges for mathematical modeling of epidemic spreading.
For instance, evidence from COVID-19 super-spreading events indicates that it is difficult to define characteristics of these events, which can vary significantly in their duration and number of people involved.
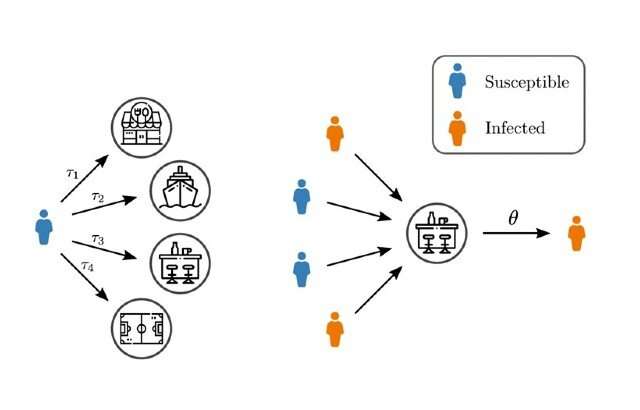
Existing network models of epidemic spreading often focus on contacts between pairs of individuals while co-location of individuals such as in the workplace, restaurants, or gym typically include more than two people. They also often fail to consider the heterogenous temporal durations of these interactions at a specific location.
In a new study, published today in Physical Review Letters, researchers developed a new approach to epidemic modeling that considers interactions between two or more people in the same location and for different amounts of time.
Challenging assumptions
The model developed by the international research team, including physicists from the University of Vermont and Université Laval, and led by Professor Ginestra Bianconi, a mathematician from Queen Mary University of London, also took into account emerging evidence that suggests a minimal infective dose is required for an infection to occur.
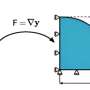
This new modeling approach radically changes well-established assumptions in epidemic network modeling, such as infection rates that are linear with the number of infected individuals. The findings show that co-locations combined with heterogeneous duration of exposure can lead to non-linear infection rates if a minimal infective dose is necessary for an infection to likely occur.
Professor Ginestra Bianconi, Professor of Applied Mathematics at Queen Mary, said: "Co-location can involve groups of people, while typically network models of epidemic spreading are based on contact networks describing pairwise interactions that can have a very different topology than co-location contact networks. Co-location also occurs in time, for example I might go to the same gym of another person but we might not always meet and we might exercise for different amount of time there."
"Our approach embraces the heterogeneities of interactions due to co-location occurring between more than two people for different amounts of time and reveal that infection kernels can be non-linear in these highly heterogeneous scenarios, meaning that if there are twice as many infected individuals visiting a given location the probability of infection can be also more than twice as big. These results shed new light on the very heterogeneous nature of super-spreading events in the context of COVID-19."
More information: Universal Nonlinear Infection Kernel from Heterogeneous Exposure on Higher-Order Networks, Physical Review Letters, doi.org/10.1103/PhysRevLett.127.158301
Journal information: Physical Review Letters
Provided by Queen Mary, University of London