When intuition fails, how to use probability and statistics to find the real answers

Imagine there's a bus that arrives every 30 minutes on average and you arrive at the bus stop with no idea when the last bus left. How long can you expect to wait for the next bus? Intuitively, half of 30 minutes sounds right, but you'd be very lucky to wait only 15 minutes.
Say, for example, that half the time the buses arrive at a 20-minute interval and half the time at a 40-minute interval. The overall average is now 30 minutes. From your point of view, however, it is twice as likely that you'll turn up during the 40 minutes interval than during the 20 minutes interval.
This is true in every case except when the buses arrive at exact 30-minute intervals. As the dispersion around the average increases, so does the amount by which the expected wait time exceeds the average wait. This is the Inspection Paradox, which states that whenever you "inspect" a process, you are likely to find that things take (or last) longer than their "uninspected" average. What seems like the persistence of bad luck is simply the laws of probability and statistics playing out their natural course.
Once made aware of the paradox, it seems to appear all over the place.
For example, let's say you want to take a survey of the average class size at a college. Say that the college has class sizes of either 10 or 50, and there are equal numbers of each. So the overall average class size is 30. But in selecting a random student, it is five times more likely that he or she will come from a class of 50 students than of 10 students. So for every one student who replies "10" to your enquiry about their class size, there will be five who answer "50." The average class size thrown up by your survey is nearer 50, therefore, than 30. So the act of inspecting the class sizes significantly increases the average obtained compared to the true, uninspected average. The only circumstance in which the inspected and uninspected average coincides is when every class size is equal.
We can examine the same paradox within the context of what is known as length-based sampling. For example, when digging up potatoes, why does the fork go through the very large one? Why does the network connection break down during download of the largest file? It is not because you were born unlucky but because these outcomes occur for a greater extension of space or time than the average extension of space or time.
Once you know about the Inspection Paradox, the world and our perception of our place in it are never quite the same again.
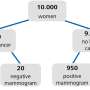
Another day you line up at the medical practice to be tested for a virus. The test is 99% accurate and you test positive. Now, what is the chance that you have the virus? The intuitive answer is 99%. But is that right? The information we are given relates to the probability of testing positive given that you have the virus. What we want to know, however, is the probability of having the virus given that you test positive. Common intuition conflates these two probabilities, but they are very different. This is an instance of the Inverse or Prosecutor's Fallacy.
The significance of the test result depends on the probability that you have the virus before taking the test. This is known as the prior probability. Essentially, we have a competition between how rare the virus is (the base rate) and how rarely the test is wrong. Let's say there is a 1 in 100 chance, based on local prevalence rates, that you have the virus before taking the test. Now, recall that the test is wrong one time in 100. These two probabilities are equal, so the chance that you have the virus when testing positive is 1 in 2, despite the test being 99% accurate. But what if you are showing symptoms of the virus before being tested? In this case, we should update the prior probability to something higher than the prevalence rate in the tested population. The chance you have the virus when you test positive rises accordingly. We can use Bayes' Theorem to perform the calculations.
In summary, intuition often lets us down. Still, by applying the methods of probability and statistics, we can defy intuition. We can even resolve what might seem to many the greatest mystery of them all—why we seem so often to find ourselves stuck in the slower lane or queue. Intuitively, we were born unlucky. The logical answer to the Slower Lane Puzzle is that it's exactly where we should expect to be!
When intuition fails, we can always use probability and statistics to look for the real answers.
More information: Leighton Vaughan Williams, Probability, Choice and Reason
Provided by Nottingham Trent University