August 28, 2020 feature
Demonstrating vortices as Brownian particles in turbulent flows
Brownian motion of particles in fluid is a common collective behavior in biological and physical systems. In a new report on Science Advances, Kai Leong Chong, and a team of researchers in physics, engineering, and aerospace engineering in China, conducted experiments and numerical simulations to show how the movement of vortices resembled inertial Brownian particles. During the experiments, the rotating turbulent convective vortical flow allowed the particles to move ballistically at first and diffusively after a critical time in a direct behavioral transition—without going through a hydrodynamic memory regime. The work implies that convective vortices have inertia-induced memory, so their short-term movement was well-defined in the framework of Brownian motion here for the first time.
Brownian motion
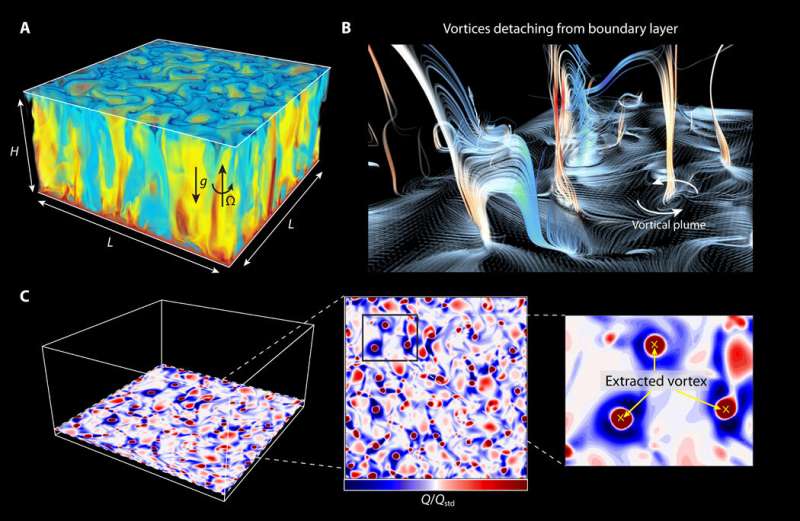
Albert Einstein first provided a theoretical explanation to Brownian motion in 1905 with the movement of pollen particles in a thermal bath, the phenomenon is now a common example of stochastic processes that widely occur in nature. Later in 1908, Paul Langevin noted the inertia of particles and predicted that their motion would be ballistic within a short period of time, changing to diffuse motion after a specific timeline. However, due to the rapidity of this transition, it took more than a century for researchers to be able to directly observe the phenomenon. Nevertheless, the "pure" Brownian motion predicted by Langevin was not observed in liquid systems and the transition spanned a broad range of time scales. The slow and smooth transition occurred due to the hydrodynamic memory effect, to ultimately generate long-range correlations. Scientists had previously observed the hydrodynamic memory effect in multiple systems including colloidal suspensions, particles suspended in air and particles trapped in optical tweezers. In this work, Chong et al. showed how vortices in highly connective flows behaved as inertial particles to perform pure Brownian motion, for the first time, without being influenced by the hydrodynamic effect. They identified and extracted the vortices using the Q-criterion (a method for vortex identification). The work will help them predict the vortex motion during a specific period of time in astrophysical and geophysical systems.
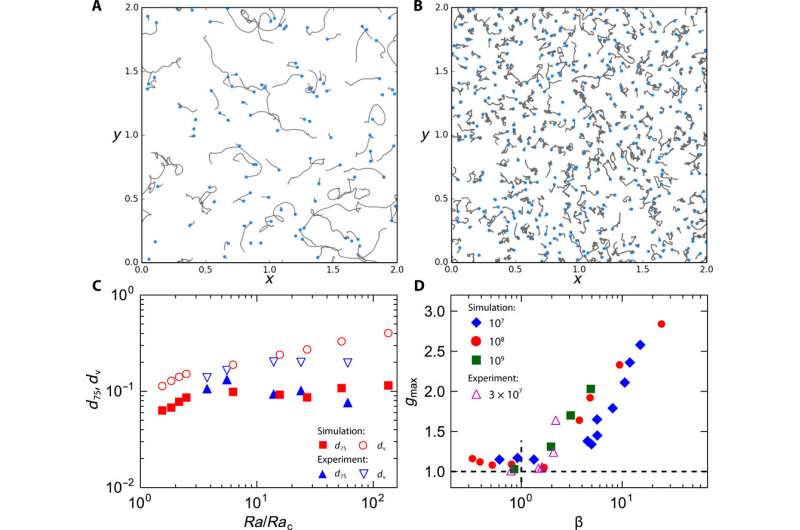
An existing challenge in astrophysical and geophysical research is to predict the movement of vortices within a specific period of time. Chong et al. used a model system to study vortices in convective flows known as the Rayleigh Benard (RB) convection, which includes a fluid layer of fixed height, heated from below and cooled from above, while being rotated about the vertical axis at an angular velocity. The temperature difference in the system destabilized the flow for convection to occur when the thermal drive was sufficiently strong. The scientists used three dimensionless parameters to characterize the flow dynamics, including the Rayleigh number (Ra), Prandtl number (Pr) and the Ekman number (Ek). In the presence of rotation, vortical structures emerged as fluid parcels spiralling up or down. Researchers continue to investigate such vortical plumes due to their importance in momentum and heat transport.
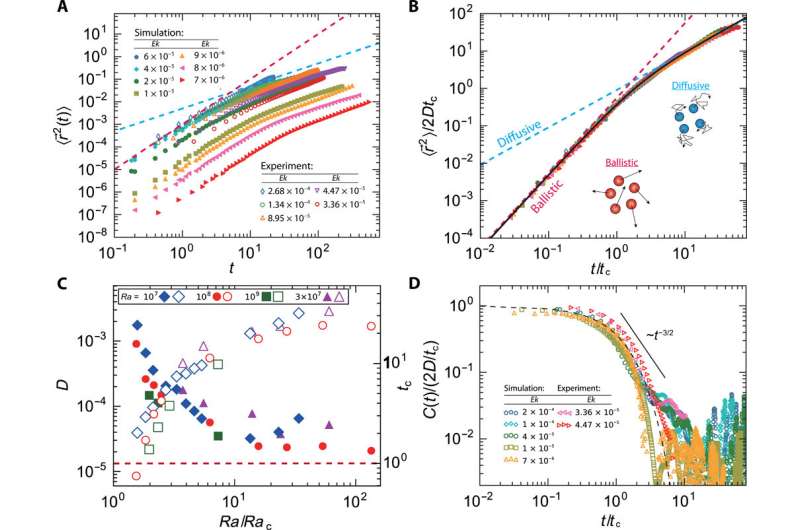
Chong et al. first studied the motion of vortices by tracking their positional change via a series of snapshots. They characterized the statistical behavior of the vortices using their mean squared displacement (MSD). The MSD values for different Ek and Ra exhibited similar behavior indicating that in a short time frame the vortex motion transferred from ballistic motion to diffusive motion. This transition resembled Brownian motion in a thermal bath. The scientists therefore treated the vortices as Brownian particles and described their motion by solving the Langevin equation to obtain their MSD. The results implied similar dynamics of vortex motion for Ra and Ek, suggesting that the vortices exhibited "pure Brownian" behavior. In the convection system, vortices carried fluid parcels that were hotter and colder than the surrounding fluid; this relatively small density difference caused by temperature variations in the experiment gave rise to the notable ballistic behavior.
Vortex distribution
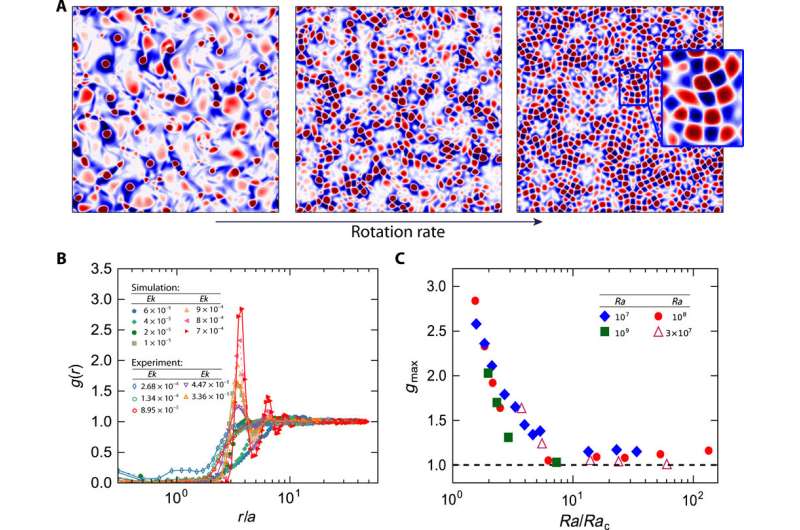
Despite Brownian-like motion, the spatial distribution of the vortices was not random, and exhibited patterned structures, which the scientists obtained using snapshots of several rotation rates. As the Ekman number (Ek) varied, several changes occurred in vortex distribution. At first, the number of vortices increased with the rate of rotation, so that the initially dilute and randomly distributed vortices became highly concentrated and clustered. The increasing vortex number density with the rotation rate also agreed with previous investigations. Next, when the rotation rate became sufficiently high, they formed a vortex-grid structure. When Chong et al. zoomed into a local region to observe the highest rotation rate, they observed a regular pattern for such vortex-grid structures. The reddish regions of the vortices formed a square lattice and the in-between bluish localized regions showed high strain behavior. The team credited the square patterns observed in the work to different boundary settings and control parameters.
Despite random motion in the temporal domain, the vortices showed a specific spatial order, which resulted in an apparent contradiction. Chong et al. observed the trajectories of vortices during slow and fast rotation. However, the vortices did not travel far enough to "see" or interact with other vortices. They credited the spatial order of the vortices to the competition between the two dynamic processes characterized by the vortex's relaxation time scale and Brownian time scale, respectively.
In this way, Kai Leong Chong and colleagues showed how the motion of vortices in rotating thermal convection resembled inertial particles performing Brownian motion. The motion underwent a sharp transition from ballistic to diffusive regions without experiencing an intermediate hydrodynamic memory region. The observation of pure Brownian motion was first predicted by Paul Langevin, although it was not previously observed in practice for inertial particles in liquid systems. The work highlighted existing classical theoretical work that showed how passive traces exhibited a transition from ballistic to diffusive behavior, similar to the experimental observations of this study. The observed pure Brownian motion also indicated the insignificance of the hydrodynamic memory effect. Chong et al. considered the Coriolis force during the study due to its relevance in vortex formation in natural phenomena, including tropical cyclones in the atmosphere, ocean vortices and the long-lived giant red spot in Jupiter. The findings will influence many situations in astrophysics, geophysics and meteorology.
More information: Kai Leong Chong et al. Vortices as Brownian particles in turbulent flows, Science Advances (2020). DOI: 10.1126/sciadv.aaz1110
Einstein, A. Investigations on the theory of the brownian movement. Annalen der Physik, www.maths.usyd.edu.au/u/UG/SM/ … /r/Einstein_1905.pdf
Rongxin Huang et al. Direct observation of the full transition from ballistic to diffusive Brownian motion in a liquid, Nature Physics (2011). DOI: 10.1038/nphys1953
Journal information: Science Advances , Nature Physics
© 2020 Science X Network