June 1, 2020 feature
A new theorem predicts that stationary black holes must have at least one light ring
Black holes, regions in space with such an intense gravitational field that no matter or radiation can escape from them, are among the most mysterious and fascinating cosmological phenomena. Over the past five years or so, astrophysicists collected the first observations of the strong gravitational forces around black holes.
The LIGO-Virgo collaboration was able to detect gravitational waves around these celestial objects using some of the most advanced gravitational-wave detectors in the world. Meanwhile, the Event Horizon Telescope research group captured the very first image of a black hole shadow.
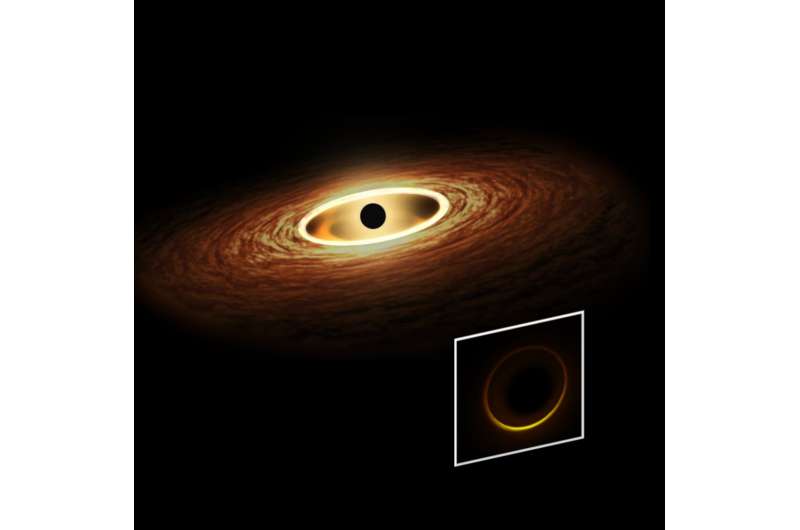
While both these observations are highly promising and captivating, neither of them is likely to unveil the event horizon, the boundary defining the specific region in space around a black hole from which nothing can escape. Nonetheless, they should contain a signature pointing to a neighboring region just outside of the event horizon, wherein light is bent so strongly that its path closes over itself and forms circular orbits known as light rings.
Studying these light rings could ultimately enrich our current understanding of black holes and their properties. So far, however, many questions remain unanswered, and we are still far from gaining a good understanding of both black holes and the light rings surrounding them.
Researchers at the Max Planck Institute for Gravitational Physics in Germany and Universidade de Aveiro in Portugal have recently introduced a theorem that makes predictions about the light rings around stationary black holes. Their theorem, presented in a paper published in Physical Review Letters, suggests that equilibrium black holes must, as a general rule, have at least one light ring in each of their sense of rotation.
"Remarkably, the properties of light rings can encode much relevant black hole information," Pedro Cunha and Carlos Herdeiro, the two researchers who carried out the study, told Phys.org via email. "Measuring these properties grants a direct window into the elusive and yet fairly uncharted regime of very strong gravity close to a black hole. At this moment it is still unclear whether Einstein's theory of general relativity remains a good description of the laws of gravity under such extreme conditions. Therefore, a key question is: does any black hole model, in any theory of gravity, need to have a light ring?"

According to the theory of general relativity, the properties of black holes in a state of equilibrium and in empty space are very constrained. Past cosmological observations suggest that these classical black holes possess light ring orbits, which could mean that any conceivable black hole would also have these orbits.
With their study, Cunha and Herdeiro tried to examine the possibility of extrapolating the notion of light ring orbits and applying it to black holes with generic matter content or to alternative theories of gravity (i.e., not the theory of general relativity). The new theorem they devised provides a solid theoretical basis for the prediction that generic equilibrium black holes must possess at least one light ring orbit.
"In our paper, we introduce a generic and mathematically innovative argument that establishes that an equilibrium black hole must indeed have, as a rule, at least one standard light ring in each rotational sense," Cunha and Herdeiro said. "To analyze light rings, typically, one considers families of solutions of a given theory of gravity, like general relativity, or some particular model of modified gravity. Here, however, the argument is of a topological nature."
Topology is a specific area of mathematics that focuses on the study of geometric properties that are not affected when an object undergoes deformations or other changes in shape and size. The key idea underlying topology studies is that some problems are unaffected by the exact shape and size of objects, but rather by the way in which these objects can be deformed into each other.
"As a simple example, a sphere and a donut have a different number of holes and are topologically distinct," the researchers explained. "In contrast, a sphere and a cube have the same topology, despite having different geometrical shapes."
In their paper, Cunha and Herdeiro apply topology-based constructs to the question of whether a light ring orbit exists around a black hole. Instead of using equations of motion provided by a specifiic theory of gravity to try and answer this question, their theorem simply examines how the spacetime should behave both near a black hole and far away from it.

"In other words, we do not assume that one law of gravity is correct, but only assume that the correct law of gravity (i.e., whichever that is) allows the existence of black holes," Cunha and Herdeiro said. "Then, forcing the spacetime structure to obey to some regularity requirements, the existence of a black hole implies that there must be a light ring outside the horizon. In fact, a rotating black hole must have at least two light rings: one for light circling the black hole in the same spinning direction as the black hole and another one for light circling the black hole in the opposite direction."
The recent paper by Cunha and Herdeiro provides a new theoretical perspective that could serve as a basis for further studies examining light rings around black holes. Its key advantage is its generality, as it does not follow any specific theory of gravity and thus holds even if Einstein's theory of general relativity was not applicable or accurate in this context.
"The prediction that black holes always have light rings and they are always outside the horizon has important consequences," Cunha and Herdeiro say. "For instance, it implies that the silhouette of a black hole, known as the black hole shadow, is generically different and usually larger than what one would expect the size of the black hole itself to be. So the shadow should always be a magnification of the black hole."
While it may be theoretically strong, just like any other mathematical theorem that applies to real systems the construct introduced by Cunha and Herdeiro is based on a series of assumptions. In their future work, the researchers plan to change some of these assumptions and assess whether their theorem's predictions change or remain the same.
"One key assumption of our theorem is that far away from the black hole there is no gravitational field," Cunha and Herdeiro said. "However, in the Universe there is a cosmological constant that drives the expansion of the Cosmos. This creates a tiny gravitational field no matter how far away from the black hole one is. It would be very interesting to understand if this slight change in assumption would change our theorem's conclusions."
More information: Pedro V. P. Cunha et al. Stationary Black Holes and Light Rings, Physical Review Letters (2020). DOI: 10.1103/PhysRevLett.124.181101
Journal information: Science Advances , Physical Review Letters
© 2020 Science X Network