April 1, 2020 feature
Optical data processing benefits from new kind of mobillity
Mode control is essential for optical communications and data processing technologies. Whether it's connections and switches in data transmission lines or some sort of non-reciprocal device for optical circuits, the ability to control, for example, whether the output mode will be even or odd for a given input mode is key. Now, researchers in China and Canada have demonstrated how to achieve efficient optical mode transfer in more compact devices than previously possible by exploiting "exceptional points" with new mobile properties.
"It is always challenging to achieve such devices with minimized volume, low insertion loss, and high efficiency," explains Bing Wang, a researcher at the Wuhan National Laboratory for Optoelectronics, Huazhong University of Science and Technology in China, and the lead author of the report of these latest results. To tackle the challenge, he and collaborators at Wuhan National Laboratory for Optoelectronics, Wuhan Institute of Technology, the Chinese Academy of Sciences Center for Excellence in Ultra-Intense Laser Science in Shanghai and the University of Ottawa investigated the behaviour of "exceptional points"—a mathematical concept that has attracted interest recently for microwave and optical guided systems because of the mode transfer possible with the topological properties they describe.
However, previous efforts to exploit exceptional points in mode transfer devices were hampered by constraints for optimizing the mode transfer efficiency and transmittance, which inevitably result in long waveguides that aren't suited for more compact applications. For the first time, Wang and his collaborators considered the possibility of exceptional points that could move. This allowed them to achieve high mode transfer efficiency and transmittance in a much shorter waveguide.
What is an exceptional point?
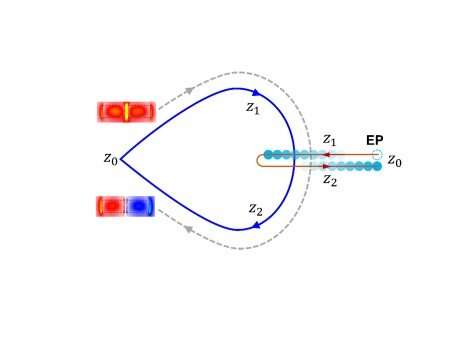
A manifold describes a topological space that locally resembles Euclidean space at each point. In real one-dimensional space, this could include lines or circles, but not figures of eight, as the crossing point would not be found in Euclidean space. Complex numbers include real and imaginary parts, where the imaginary part is proportional to the square root of 1 and is often used to describe damping behaviour in physical systems. Because of the two components, a one-dimensional complex manifold is presented as a plane called a Riemann surface, which might represent eigenvalues of the energy of a particular mode in a system with dissipation. The exceptional point is the branching singularity where two modes meet, and this is the topological property that allows mode transfer in the system.
Wang and colleagues fabricated waveguides with two gratings etched into silicon on silicon oxide. The corrugations at the grating edges affect the effective loss of the system. If plots of the grating width and grating separation encircle the coordinates of the exceptional point, mode transfer occurs, so an odd or even mode input results in an odd or even mode output depending on the system parameters. However, either the exceptional point is near the entrance end of the waveguide so that the eigenvalues easily encircle it for efficient mode transfer, but the transmittance is low due to the high loss of the system. Alternatively, the exceptional point is far from the waveguide entrance so that the mode transfer efficiency is compromised unless the waveguide is much longer.
Moving to the groove
Wang and colleagues got around the trade-off between waveguide length and performance by varying the width and separation of the gratings, which allowed the exceptional points to move. "Moving exceptional points is a conceptional breakthrough since they are originally considered in a two-dimensional parameter space," explains Wang, who was surprised himself at how the approach worked.
In fact, he and his colleagues had been focused on reducing the loss with stable exceptional points by changing the grating corrugations of the waveguides. "In this way, however, we noticed that the exceptional point is no longer fixed," Wang tells phys.org. Having developed the theory to explain the effect, they were able to confirm their results with numerical simulations.
They expect the effect to be useful for optical convertors, couplers, filters and switches in integrated devices, as well as broadband optical isolators and circulators, which bring electronic-like direction bias to optical circuits. They also believe it should apply to acoustic and matter waves.
Next, they plan to manipulate the exceptional points in real time. LiNbO3 has a strong electro-optic effect, so they could manipulate the effective permittivity of the waveguide by changing an external electric field.
More information: Qingjie Liu et al. Efficient mode transfer on a compact silicon chip by encircling moving exceptional points, Physical Review Letters (2020) accepted manuscript journals.aps.org/prl/accepted/ … c48d77b7bc25154f9a8c
Journal information: Physical Review Letters
© 2020 Science X Network