New artificial neural network model bests MaxEnt in inverse problem example
Numerical simulations, generally based on equations that describe a given model and on initial data, are being applied in an ever-expanding range of scientific disciplines to approximate processes at given points in time and space. With so-called inverse problems, this critical data is missing—researchers must reconstruct approximations of the input data or of the model underlying observable data in order to generate the desired predictions.
While techniques for doing so already exist, they are ill-defined, unable to assign unique interpretations or values to a given point. As an example, in the most commonly used method for solving such problems, the so-called maximum entropy (MaxEnt) approach, prior knowledge is added by specifying a default distribution that corresponds to expected results in the absence of data. The algorithm iteratively searches for a distribution that maximizes entropy with respect to this default distribution while also generating a function close to existing data. The approach includes a parameter used to weigh the relative importance between the entropy and the error terms. There are several methods for fixing it that often yield different results when applied in practice.
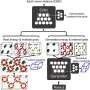
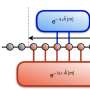
In the paper Artificial Neural Network Approach to the Analytic Continuation Problem, QuanSheng Wu, a scientist and Romain Fournier, a master's student at EPFL's C3MP, led by Professor Oleg Yazyev, and colleague Professor Lei Wang at the institute of Physics of the Chinese Academy of Sciences present a supervised learning approach to the problem. Based on an artificial neural network (ANN)—highly versatile thanks to an ability to approximate continuous functions under mild assumptions and because of powerful libraries allowing for the efficient implementation of different ANN architectures that can be tailored to take advantage of data structures—the new method appears to be as accurate as MaxEnt and considerably cheaper computationally.
In a first test of the ANN framework, the researchers chose to examine a system that has an analytical solution, but is difficult to solve using MaxEnt—namely, the time-correlation function of the position operator for a harmonic oscillator linearly coupled to an ideal environment. The Hamiltonian, or operator generally corresponding to the total energy of the system, is known in this case, and the data of interest—the imaginary-time correlation function—can be generated by quantum Monte Carlo (QMC) simulations.
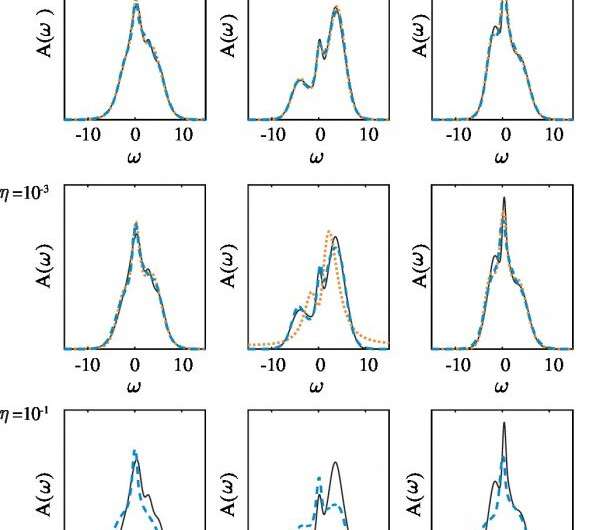
The analytic solution gives the relation of the power spectrum to an imaginary-time correlation function and as such provided physically relevant training data for the ANN model. The researchers trained the ANN with the generated data and then tested it by obtaining the imaginary-time correlation function calculated in the earlier step by QMC. The model trained on the entire dataset showed almost perfect agreement with the analytic solution. MaxEnt failed to give accurate results, though the researchers noted that better results would likely have been obtained by computing the correlation function on a larger number of points.
To further test the model in a practical way, the researchers looked to recover the electron single-particle spectral density in the real frequency domain from a Green's function in the imaginary time domain. While both the ANN and the MaxEnt models were able to predict starting spectral functions accurately for the lowest level of noise, MaxEnt tended to suppress peaks in the predicted spectral function with increasing noise in the system. These results show that the ANN model is versatile and robust against noisy data.
The new method is also computationally more efficient. ANN allowed direct mapping between Green's functions and the spectral densities and can in that sense solves the problem directly. MaxEnt on the other hand is iterative and generates trial functions until convergence is reached. With the computational set-up used in the paper, the time required for converting a given number of pairs at a given level of noise was 5 seconds in the case of ANN compared with the 51 minutes that MaxEnt would have needed using the same setup.
The researchers said that such ANNs are likely to be able to solve other inverse problems, provided that relevant datasets—derived, for instance, using available experimental results combined with data augmentation techniques—can be constructed. The trained models resulting from the work can be obtained from a public repository at GitHub here: github.com/rmnfournier/ACANN.
More information: Romain Fournier et al, Artificial Neural Network Approach to the Analytic Continuation Problem, Physical Review Letters (2020). DOI: 10.1103/PhysRevLett.124.056401
Journal information: Physical Review Letters
Provided by National Centre of Competence in Research (NCCR) MARVEL