Mathematicians help improve efficiency of data centers using Markov chains
RUDN University mathematicians created a model of maximum efficiency of data centers. It is based on a nontrivial Markov chain. In addition to the obvious practical applications of the results for the organization of servers and data centers, the theoretical part will be useful for the theory of queues and queuing, as well as for working with big data and neural networks. The study is published in the journal Mathematics.
A data center is a system of servers, and their task is to provide computing resources and disk space at the request of users. The higher the load, the more equipment heats up. Servers may temporarily stop working if they overheat. The temperature level that corresponds to the overheating point is called the first critical level. The second is the level to which the temperature of the server must fall for it to resume (at least partially) the work.
These levels are different. For example, if each user loads the server so that the temperature of its processor grows by 0.1 degrees, and the first critical level is 100 degrees, the second critical level should be set no higher than 99.9 degrees. If put above, the first request of the user will overheat the server again. In this case, the two critical levels should be located close enough to each other—if their difference is large, the server capacity will not be used completely. It is necessary to configure these levels so that the servers of the data center do not shut down constantly due to overheating and at the same time work with a full load.
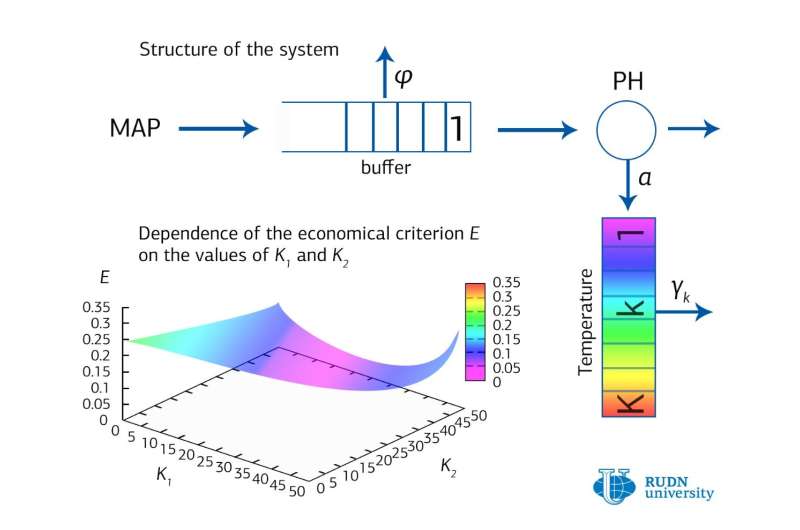
RUDN University mathematicians Olga Dudina and Alexander Dudin were able to find a solution to the optimization problem, which ensures that the servers work at full capacity but do not overheat. Its condition looks like this: depending on a random process that simulates the flow of users, place two critical levels to prevent overheating, but the computation power would be used to the maximum. At the same time, partial inactivity is allowed, that is, if the second critical temperature level is exceeded, some requests from users are rejected.
The mathematicians solved probabilistic equations for different values of critical levels. As a random process that simulates the arrival of users, RUDN University mathematicians used the Markov chain. The simplest example of such a chain is a random walk of a point along a straight line. Every second, a coin is tossed: if heads come up, the point moves 1 cm forward; if tails, 1 cm back. Time is discrete in this process—that is, changes occur once a second, and the position of the point in the future depends only on its current position and the result of the coin toss.
To test the effectiveness of their method, RUDN University mathematicians conducted a numerical experiment that simulated the behavior of the server. Its results were evaluated using indicator E, a quality criterion that determines losses for denial of service to the user and overheating of equipment per unit of time. It turned out that the new method allows more than ten times—from 0.31 to 0.03—to reduce the loss of the simulated server and significantly increase the efficiency of the data center.
Also, the Markov chain, which originated in the work of mathematicians, has some interesting properties. In addition to its applications in IT, their model will be useful in Queueing theory. This theory is necessary for solving queuing problems, working with big data and neural networks.
More information: Olga Dudina et al, Optimization of Queueing Model with Server Heating and Cooling, Mathematics (2019). DOI: 10.3390/math7090768
Provided by RUDN University