Log-periodic quantum oscillations and discrete scale invariance in Dirac materials
One fundamental problem of quantum electrodynamics is the fate of the superheavy atomic nucleus, which is proposed to collapse when the atomic number exceeds certain value. However, this intriguing supercritical collapse phenomenon remains elusive in experiments. Discrete scale invariance (DSI) is a scale anomaly with the violation of the continuous scale symmetry. The intriguing log-periodicity is the characteristic signature of DSI, which exists in rupture, growth processes, turbulence, finance, and so on. The DSI feature is of high interest in quantum physics, while it can be rarely realized in quantum systems experimentally. The previously known example with DSI in quantum physics only focuses on the Efimov trimer state.
A novel type of quantum magneto-resistance oscillations has been observed in topological material ZrTe5 (Science Advances 4, eaau5096 (2018)), constituting the third known distinctive type of periodicity in the nearly 90 years searching for quantum oscillations in solids. Moreover, the discovery of the exotic logB periodic oscillations can virtually represent the discrete scale invariance associated with the quasi-bound states formed through supercritical atomic collapse in Dirac materials. Such peculiar feature is supposed to be universal in Dirac materials with Coulomb attraction. Thus, it is desirable to extend the investigations to other topological systems, and more importantly to other physical observables. In a new work published in the National Science Review, Beijing-based research collaboration led by Prof. Jian Wang, Prof. Haiwen Liu and Prof. Jiyan Dai has revealed the universality of the log-periodic quantum magneto-oscillations and DSI phenomenon in Dirac materials by magneto-transport results of HfTe5 crystals.
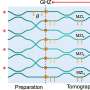
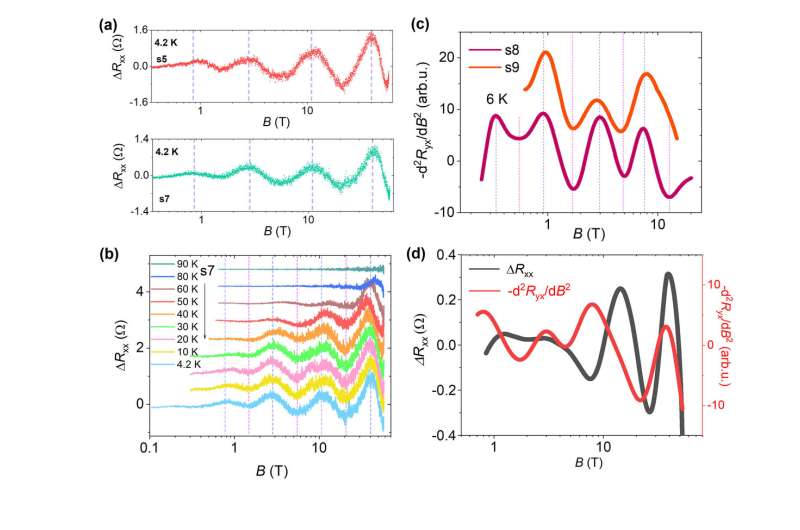
Scientists measured the magneto- and Hall resistance of the HfTe5 crystals at pulsed magnetic fields up to 58 T and static magnetic fields up to 25 T. Clear logB-periodic quantum oscillations signaling of DSI are observed in the longitudinal magneto-resistance (MR) (subfigure (a)), independent on the minor differences of the sample quality. The temperature dependence of the logB-periodic oscillations in HfTe5 is shown in subfigure (b). One can see that the log-periodic features become invisible when the temperature is increased to be above 80 K. Furthermore, for the first time, the DSI signal with remarkable logB-periodicity is discovered in the Hall traces of the HfTe5 crystals. The finding indicates an overall effect of the DSI feature on the transport properties of the system. The second derivate results of the Hall data are shown in the subfigure (c). In addition, the MR and Hall results on the same sample are shown in subfigure (d). It is found that in the oscillations the phase of Hall data is slightly ahead of MR, reminiscent of that in the two-dimensional quantum Hall effect.
The log-periodic oscillations in Dirac materials were attributed to the supercritical atomic collapse phenomenon and the concomitant quasi-bound states featuring discrete scale invariance in Dirac materials. The quasi-particle in Dirac materials obeys the relativistic equation, and the Fermi velocity is much smaller than the speed of light in vacuum. Thus, the value of the fine-structure constant in Dirac materials is much larger than that in vacuum, which provides a promising platform to investigate the supercritical atomic collapse phenomenon. Owing to the large value of the fine-structure constant in these solid state systems, the Coulomb attraction gives rise to the supercritical atomic collapse in analogy to the phenomenon proposed to exist in superheavy atoms. Moreover, the massless Dirac equation with Coulomb attraction preserves the discrete scale invariance, in contrast to the discrete scale symmetry breaking in massive Dirac equation of superheavy atoms.
In topological material HfTe5, the log-periodic quantum oscillations in both the longitudinal MR and the Hall resistance are closely related to the quasi-bound states of Weyl particles from the hole band with long-range Coulomb attraction when the carrier density is so dilute, and the long-range Coulomb attraction is generated by the charge impurity or the opposite type of carriers. Aside from the quasi-bound states near the Coulomb center, large number of mobile carriers also exist in the Fermi surface. Thus, the resonant scattering between the mobile carriers and the quasi-bound states around the Fermi level determine the transport properties of the material, e.g. the longitudinal MR and the Hall traces. Further theoretical analysis signify that the π/2 phase shift originates from the resonant scattering between the mobile carriers and the quasi-bound states, sharing the same origin of the log-periodic oscillations. Moreover, scientists have analyzed the influence of a small band gap on the DSI feature and clarified its relevance to various topological materials.
Dirac materials showing log-periodicity provide promising platforms to investigate the rarely observed supercritical atomic collapse phenomenon and the discrete scale invariance feature. This work provides new insights towards further understanding of the universality and the physical nature of the log-periodic quantum oscillations in Dirac materials.
More information: Huichao Wang et al, Log-periodic quantum magneto-oscillations and discrete scale invariance in topological material HfTe5, National Science Review (2019). DOI: 10.1093/nsr/nwz110
Provided by Science China Press