At the edge of chaos: New method for exoplanet stability analysis
Exoplanets revolving around distant stars are coming quickly into focus with advanced technology like the Kepler space telescope. Gaining a full understanding of those systems is difficult, because the initial positions and velocities of the exoplanets are unknown. Determining whether the system dynamics are quasi-periodic or chaotic is cumbersome, expensive and computationally demanding.
In this week's Chaos, Tamás Kovács delivers an alternative method for stability analysis of exoplanetary bodies using only the observed time series data to deduce dynamical measurements and quantify the unpredictability of exoplanet systems.
"If we don't know the governing equations of the motion of a system, and we only have the time series—what we measure with the telescope—then we want to transform that time series into a complex network. In this case, it is called a recurrence network," Kovács said. "This network holds all of the dynamical features of the underlying system we want to analyze."
The paper draws on the work of physicist Floris Takens, who proposed in 1981 that the dynamics of a system could be reconstructed using a series of observations about the state of the system. With Takens' embedding theorem as a starting point, Kovács uses time delay embedding to reconstruct a high-dimensional trajectory and then identify recurrence points, where bodies in the phase space are close to each other.
"Those special points will be the vertices and the edges of the complex network," Kovács said. "Once you have the network, you can reprogram this network to be able to apply measures like transitivity, average path length or others unique to that network."
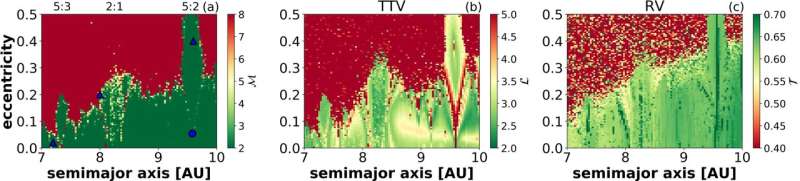
Kovács tests the reliability of the method using a known system as a model, the three-body system of Saturn, Jupiter and the sun, and then applies it to the Kepler 36b and 36c system. His Kepler system results agree with what is known.
"Earlier studies pointed out that Kepler 36b and 36c is a very special system, because from the direct simulation and the numerical integrations, we see the system is at the edge of the chaos," Kovács said. "Sometimes, it shows regular dynamics, and at other times, it seems to be chaotic."
The author plans to next apply his methods to systems with more than three bodies, testing its scalability and exploring its ability to handle longer time series and sharper datasets.
More information: Recurrence network analysis of exoplanetary observables, Chaos, DOI: 10.1063/1.5109564
Journal information: Chaos
Provided by American Institute of Physics