'The Big Bang Theory' takes math notes from Carl Pomerance
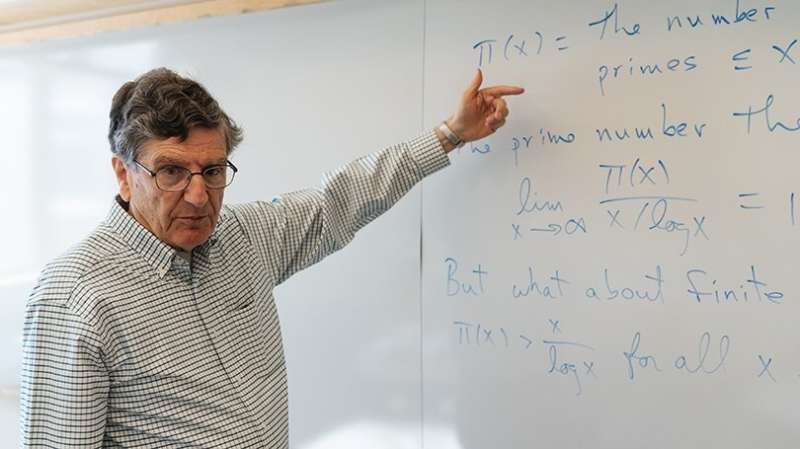
A prime number theory equation by mathematics professor emeritus Carl Pomerance turned up on The Big Bang Theory, where it was scrawled on a white board in the background of the hit sitcom about a group of friends and roommates who are scientists, many of them physicists at the California Institute of Technology.
In a recent paper, "Proof of the Sheldon Conjecture," Pomerance, the John G. Kemeny Parents Professor of Mathematics Emeritus, does the math on a claim by fictional quantum physicist Sheldon Cooper that 73 is "the best number" because of several unique properties. Pomerance's proof shows that 73 is indeed unique.
The Big Bang Theory is known for dressing the set with "Easter eggs" to delight the self-avowed science nerds in the audience. When UCLA physics professor David Saltzberg, technical consultant for The Big Bang Theory, heard about the Sheldon proof, he contacted Pomerance to ask if they could use it in the show, which was broadcast April 18.
"What's interesting is, when you see cartoons with technical stuff on boards, usually it doesn't make any sense, but the stuff that they have on the boards, I'll usually say, oh, I recognize that," says Pomerance, who wasn't particularly a fan of the show before he came across the "Sheldon prime number problem" while doing some light math reading.
What is it about the number 73 that makes it so attractive to Sheldon, who includes a T-shirt emblazoned with the number in his regular shirt rotation? Pomerance and co-author Chris Spicer, associate professor of mathematics at Morningside College, explain in the introduction to the proof, accepted for publication in American Mathematical Monthly. One note of context: The "index" of a prime number is its place in ascending numerical order. (For example, the consecutive prime numbers 2, 3, 5, 7 are indexed 1, 2, 3, and 4.)
"First note that not only is 73 a prime number, its index in the sequence of primes is the product of its digits, namely 21; it is the 21st prime. In addition, reversing the digits of 73, we obtain the prime 37, which is the 12th prime, and 12 is the reverse of 21," they write, laying out the points Sheldon makes on the show.
The question Pomerance and Spicer set out to solve is whether this is the only prime number with these properties. Since there is, theoretically, an infinite number of prime numbers, that is easier said than proved. Their paper proposes a series of equations that they say proves 73 is, in fact, unique. It is a portion of this proof, which runs 10 pages, that is written on a whiteboard on the show's set.
"It's like the show within the show. It has nothing at all to do with the plot. It's just in the background. It's difficult to see it. Sometimes it's a little fuzzy, it's at an angle, there's a character blocking it. But if you know to look for it—hey, that's my paper," Pomerance says.
Provided by Dartmouth College