Epidemiological model lends insight to chlamydia outbreak in Japan
Mathematical models that quantify the dynamics of infectious diseases are crucial predictive tools for the control of ongoing and future outbreaks. An infection's basic reproduction number (R0) is especially important to disease modeling and epidemiology, as it determines global behavior and measures a disease's transferability within a fully-susceptible population. In short, R0 helps public health officials discern an epidemic's intensity and the likelihood of its successful spread. If R0>1, an outbreak occurs. If R0<1, the infection typically dies out.
Sometimes a disease is endemic, meaning that it is continuously present and maintained at a baseline level in a specific location. In these cases, the number of infective individuals remains nearly static and in endemic equilibrium. Chlamydia, a sexually transmitted disease in both men and women that can cause significant damage to a woman's reproductive system, has been endemic in Japan since 2012. To mathematically estimate R0 for chlamydia's pervasiveness in Japan, one must clarify the stability of the corresponding model's endemic equilibrium.
In an article publishing on February 19th in the SIAM Journal on Applied Mathematics, a publication of the Society for Industrial and Applied Mathematics, Toshikazu Kuniya studies the global behavior of a multi-group SIR epidemic model with age structure and uses the model to estimate R0 for Japan's chlamydia outbreak. Kuniya has been modeling infectious diseases since he was a master's student and is especially curious about their global behavior. "I have recently become interested in the application of epidemic models to their epidemiological considerations," he said. "I think the global behavior of epidemic models plays an important role in understanding infectious disease data in the long-time scale."
An SIR model—which stands for susceptible, infective, and recovered—is a simple compartmental model and one of the most basic mechanisms of mathematical epidemiology. It divides the total population of an affected area into the three aforementioned classes. This type of model converges to a disease-free equilibrium when R0<1 and an endemic equilibrium when R0>1.
While Kuniya's model is quite similar to one employed by previous researchers, Kuniya reformats it into a multi-group model with age-dependent susceptibility. "I chose a multi-group SIR epidemic model with age structure because it is useful to handle the data with the heterogeneity (sex, age, position, etc.) of each person," he said. "The age structure enables us to consider the effects of the demographic age distribution's time variation and the age-dependency of each epidemic parameter."
For the sake of simplicity, Kuniya assumes that the sum of the mortality and recovery rates is constant. He also weakens some of the prior model's restrictive assumptions that prevented successful application. "Under the previous assumption, the disease transmission coefficient was independent of the state of infective individuals," Kuniya said. "In this study, we have weakened this assumption to be able to consider the disease transmission coefficient's possible dependence on the state of infective individuals. By virtue of this, we can model the disease transmission from male individuals to female individuals and vice versa." Doing so allows him to prove that R0 completely determines the model's global behavior. It also eliminates the possibility of an unstable endemic equilibrium if R0>1.
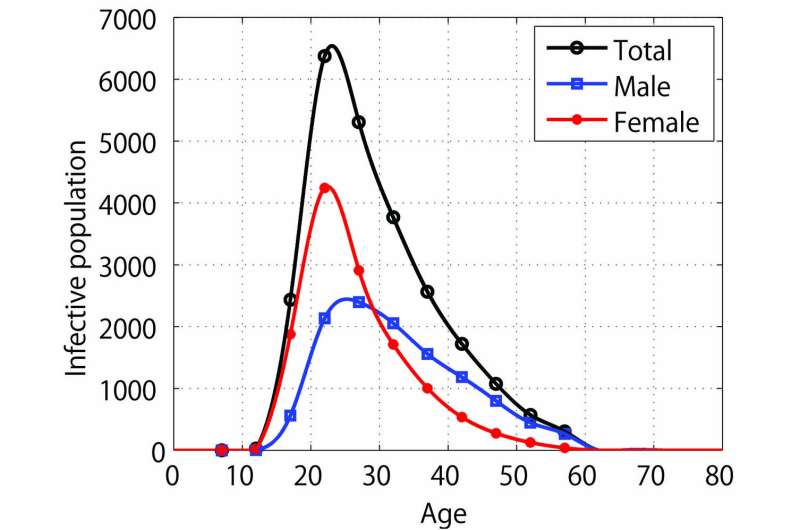
After establishing his model, Kuniya applies it to the 2015 manifestation of chlamydia in Japan, for which there is an available heterogeneous dataset arranged by age and sex. Chlamydia's seemingly endemic state in recent years also made the disease an appropriate target. Kuniya examines four particular cases—in the form of a homogenous model, an age-independent two-sex model, an age-dependent one-sex model, and an age-dependent two-sex model—and compares the estimated results of R0. These special cases yield an R0 estimate between 1.0148 and 1.0535 for chlamydia in Japan. His analysis also reveals that introduction of an age structure impacts the value of R0 more strongly than application of a two-group structure. This indicates that ordinary differential equation models lacking age structure—while typically easier to use than partial differential equation models with age structure—might ultimately underestimate R0.
Throughout the course of his investigation, Kuniya assumes that all infective individuals are documented, when in reality some occurrences of chlamydia likely go unreported—especially because the disease often shows no symptoms. This discrepancy may have led to underestimated R0 values for the four individual cases. Accounting for unreported cases and improving the estimation's overall accuracy is a task for forthcoming study.
In the future, Kuniya hopes to apply his findings to more general models with more than two groups, which requires an increasingly elaborate dataset. "I think we can improve the estimation of R0 and other epidemic parameters by using a more detailed dataset subdivided according to the heterogeneity—for instance, sexual activity—of each individual," he said. "We can apply our theoretical results to more general cases with arbitrary numbers of groups."
More information: SIAM Journal on Applied Mathematics (2019). DOI: 10.1137/18M1205947
Journal information: SIAM Journal on Applied Mathematics
Provided by Society for Industrial and Applied Mathematics