Physicists demonstrate magnetometer that uses quantum effects and machine learning

Researchers from the Moscow Institute of Physics and Technology (MIPT), Aalto University in Finland, and ETH Zurich have demonstrated a prototype device that uses quantum effects and machine learning to measure magnetic fields more accurately than its classical analogues. Such measurements are needed to seek mineral deposits, discover distant astronomical objects, diagnose brain disorders, and create better radars.
"When you study nature, whether you investigate the human brain or a supernova explosion, you always deal with some sort of electromagnetic signals," explains Andrey Lebedev, a co-author of the paper describing the new device in npj Quantum Information. "So measuring magnetic fields is necessary across diverse areas of science and technology, and one would want to do this as accurately as possible."
Quantum magnetometer offers more precision
A magnetometer is an instrument that measures magnetic fields. A compass is an example of a primitive magnetometer. In an electronics store, one can find more advanced devices of this kind used by archaeologists. Military mine detectors and metal detectors at airports are also magnetometers.
There is a fundamental limitation on the accuracy of such instruments, known as the standard quantum limit. Basically, it says that to double the precision, a measurement has to last four times as long. This rule applies to any classical device, which is to say one that does not utilize the bizarre effects of quantum physics.
"It may seem insignificant, but to gain 1,000 times in precision, you would have to run the experiment 1 million times longer. Considering that some measurements take weeks to begin with, chances are you will experience a power cut or run out of funds before the experiment is over," says Lebedev, who is a leading researcher at the Laboratory of the Physics of Quantum Information Technology, MIPT.
Achieving a higher accuracy, and therefore shorter measurement times, is crucial when fragile samples or living tissue is examined. For example, when a patient undergoes positron emission tomography, also known as a PET scan, radioactive tracers are introduced into the bloodstream, and the more sensitive the detector is, the smaller the necessary dose.
In theory, quantum technology enables a measurement's accuracy to be increased twofold by repeating it twice instead of four times as in the case of a classical magnetometer. The paper reported in this story details the first successful attempt to put this principle into practice using a superconducting qubit as the measuring device.
Qubits measure magnetic fields
A qubit is a particle that obeys the laws of quantum physics and can occupy two discrete basis states simultaneously in what is known as a superposition. This notion refers to a multitude of "intermediate" states, each of which collapses into one of the two basis states as soon as it is measured. An example of a qubit is a hydrogen atom whose two basis states are the ground and the excited state.
In the study by Lebedev and co-authors, the qubit was realized as a superconducting artificial atom, a microscopic structure made of thin aluminum films and deposited on a silicon chip held in a powerful refrigerator. At temperatures close to the absolute zero, this device behaves as an atom. In particular, by absorbing a specific portion of microwave radiation fed to the qubit via a cable, it can enter a balanced superposition of the two basis states. If the state of the device is then checked, the measurement will detect the ground and the excited state with an equal 50 percent probability.
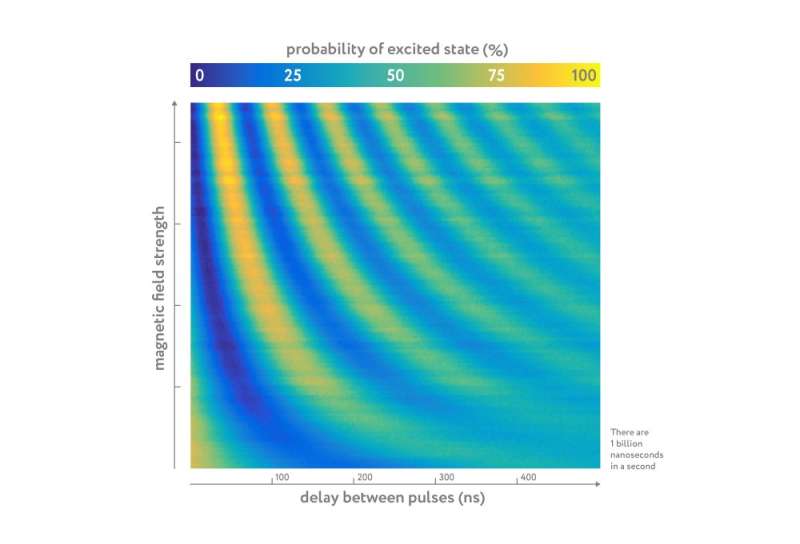
Superconducting qubits are distinguished by their sensitivity to magnetic fields, which can be used for making measurements. Once a suitable microwave radiation pulse is used to drive the device into a balanced superposition of the ground and excited states, this new state begins to change predictably with time. To track this state change, which is a function of the external magnetic field, the researchers sent a second microwave pulse to the device after a brief delay and measured the probability of finding the qubit in the excited state. This probability, which was calculated over many identical experiments performed in quick succession, indicates the strength of the magnetic field. The precision of this quantum technology surpasses the standard quantum limit.
Qubit training
"An actual physical qubit is imperfect. It is a manmade device, rather than a mathematical abstraction. So instead of using a theoretical formula, we train the qubit before making real measurements," says Lebedev. "This is the first time machine learning has been applied to a quantum magnetometer," he adds.
Qubit training consists of making many preliminary measurements under controlled conditions with predetermined delays between pulses and in a range of known magnetic fields. The authors thereby determined the probability of detecting the excited state following the sequence of two pulses for an arbitrary field and pulse delay. The researchers plotted their findings on a diagram, which serves as a fingerprint for the individual device used in the study, accounting for all its imperfections.
The point of the sample fingerprint is that the delay times between pulses can be optimized during repeated measurements. "We perform adaptive measurements," says Lebedev. "At the first step, we take a measurement given a certain delay between the microwave pulses. Then, depending on the result, we let our pattern recognition algorithm decide how to set the delay for the next iteration. This results in a higher precision over fewer measurements."
Qubits in the lab, hospital, and outer space
So far, the prototype device and superconducting qubits work only at about 0.02 degrees above absolute zero, which is defined as −273.15 degrees Celsius. "This is some 15,000 times colder than room temperature," Lebedev points out. "Engineers are working on increasing the operating temperature of such devices to 4 kelvins [−269 C]. This would make cooling by liquid helium feasible, making the technology commercially viable."
The prototype has been tested on a static magnetic field, but time-varying or transient fields can be measured in the same way. The research team is already conducting experiments with variable fields, expanding the potential range of applications of their device.
For example, a quantum magnetometer could be mounted on a satellite to observe astronomical phenomena too faint for classical instruments. Conveniently, the frigid space conditions make cooling somewhat less of an issue. Besides, a system of quantum magnetometers could work as an ultrasensitive radar. Further applications of such nonclassical instruments include MRI scans, mineral prospecting, and research into biomolecule structure and inorganic materials.
How to extract information about the external field from a qubit
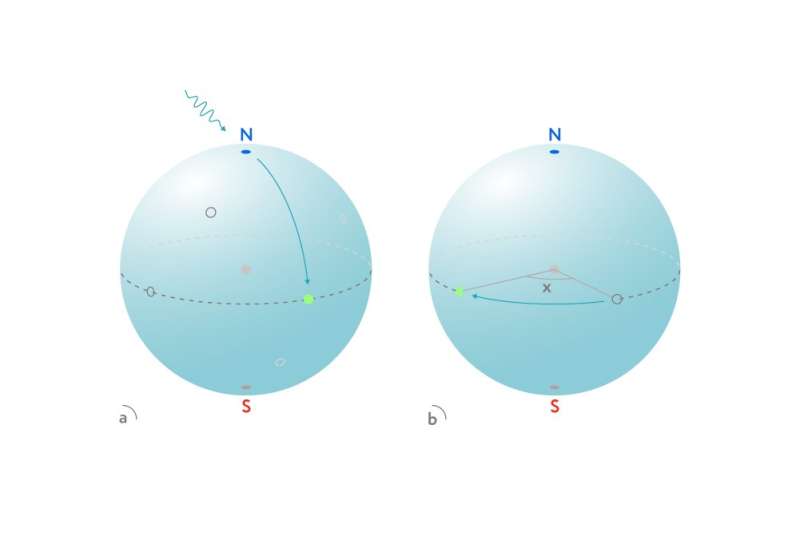
Once the first microwave pulse is absorbed by the magnetometer, it enters a superposition of the ground and excited states. This can be visualized by picturing the two basis states of the qubit as the two poles of a sphere, where each other point on the sphere represents some state of superposition. In this analogy, the first pulse drives the state of the qubit from the north pole—the ground state—to some point on the equator (figure 2a). A direct measurement of this state of balanced superposition would result in the ground or excited state being detected with even odds.
Following the first pulse, the qubit becomes sensitive to the external field. This is manifested as a predictable change of the device's quantum state. It can be pictured as a point rotating along the equator of a sphere (figure 2b). How fast this point rotates, depends on the strength of the external field. This means that by finding a way to measure the angle of rotation X over a known period of time, the field can be quantified.
The main challenge is to distinguish between the different states on the equator: Unless some trick is used, the measurement would return the excited state exactly 50 percent of the time. This is why the physicists sent a second microwave pulse to the qubit and only then checked its state. The idea behind the second pulse is that it predictably shifts the state of the device off the equator, into one of the hemispheres. Now, the odds of measuring an excited state depend on how much the state has rotated since the first pulse, that is, angle X. By repeating the sequence of two pulses and a measurement many times, the authors calculated the probability of an excited state, and thus the angle X and the strength of the magnetic field. This principle underlies the operation of their magnetometer.
More information: S. Danilin et al. Quantum-enhanced magnetometry by phase estimation algorithms with a single artificial atom, npj Quantum Information (2018). DOI: 10.1038/s41534-018-0078-y
Provided by Moscow Institute of Physics and Technology