Mathematician discusses solving a seemingly unsolvable equation
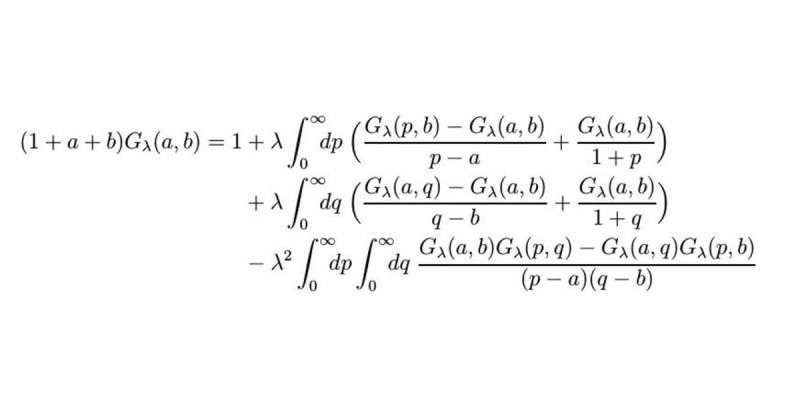
After 10 years, Prof. Raimar Wulkenhaar from the University of Münster's Mathematical Institute and his colleague Dr. Erik Panzer from the University of Oxford have solved a mathematical equation which was considered to be unsolvable. The equation is to be used to find answers to questions posed by elementary particle physics. In this interview with Christina Heimken, Wulkenhaar looks back on the challenges encountered in looking for the formula for a solution and he explains why the work is not yet finished.
You worked on the solution to the equation for 10 years. What made this equation so difficult to solve?
It's a non-linear integral equation with two variables. Such an equation is so complex that you do actually think there can't possibly be any formula for a solution. Two variables alone are a challenge in themselves, and there are no established approaches for finding a solution for non-linear integral equations. Nevertheless, again and again during those 10 years there were glimmers of hope and as a result, and despite all the difficulties, I thought finding an explicit formula for a solution – expressed through known functions – was actually possible.
What can the equation be used for?
It's about a mathematical understanding of quantum field theories. These belong to the field of physics and play a part in large-scale experiments such as those carried out at CERN. The aim is to mathematically describe elementary particles, i.e. the smallest known components of matter. But this is so complicated that, instead, imaginary particles are described mathematically which have certain properties of the real particles. The hope is that one day the real particles can be described using the methods established in this way.
After working on the problem for 10 years, you experienced a breakthrough this year. How did that come about?
Towards the end of May, I tried out an idea for which my Ph.D. student, Alexander Hock, provided the decisive impulse. I worked out a new equation – simpler than the previous one – and began to solve it in loops. What this means is that you approach the solution step by step, i.e. loop by loop, by calculating the left side of the equation in each previous step and using it for the right side of the equation in the next step.
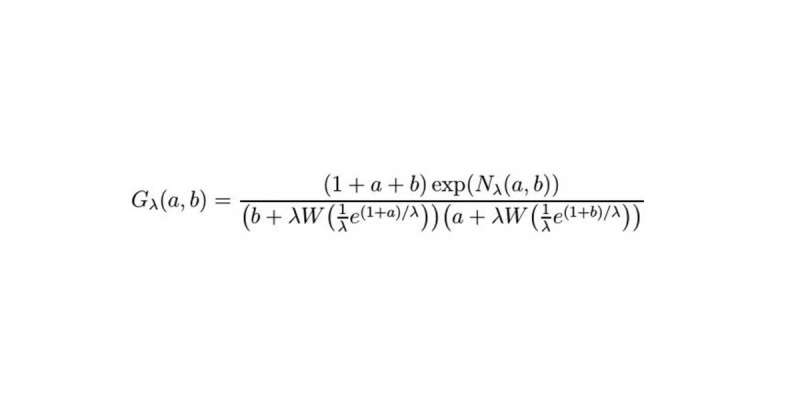
In the fourth loop I had to calculate a sum of 46 integrals which contained amongst other things polylogarithms. These polylogarithms, which are some of the more demanding functions, became more complicated in each loop. I was lucky in that, in sum, almost everything was cancelled out, and what remained was only a short sum of powers of normal logarithms. I immediately realized that there was treasure to be found here.
The fifth loop was not so easy to solve – but again I was lucky. During a summer school in the French Alps I had the opportunity of talking to experts on such functions. One of these experts was Dr. Erik Panzer from the University of Oxford. He had written a computer programme on the symbolic mathematics of hyperlogarithms and he provided support. Overnight this programme calculated my equation through to the seventh loop. It confirmed my results through to the fourth loop, and after the fourth loop the miracle continued – everything could be broken down into normal logarithms. A pattern began to emerge!
What does that mean?
Perhaps you remember Pascal's Triangle from your schooldays, with the binominal coefficients? In the triangle, every number entered in a line of the triangle is the sum of the two numbers entered above it. And it is just such a triangular structure that we find in our loops – if more complicated than in Pascal's triangle.
On June 9, loops eight and nine were completed. And then came what was perhaps the most important moment. Erik Panzer deciphered a so-called recursive formula, which generates each last line in the triangle from the line above it, and which thus enables us to extrapolate from the known to the unknown.
What went through your mind in this moment?
One of the things I thought was, "No one can be this lucky." I realized that we would solve the equation. At our evening meal there was a bottle of wine for our table …
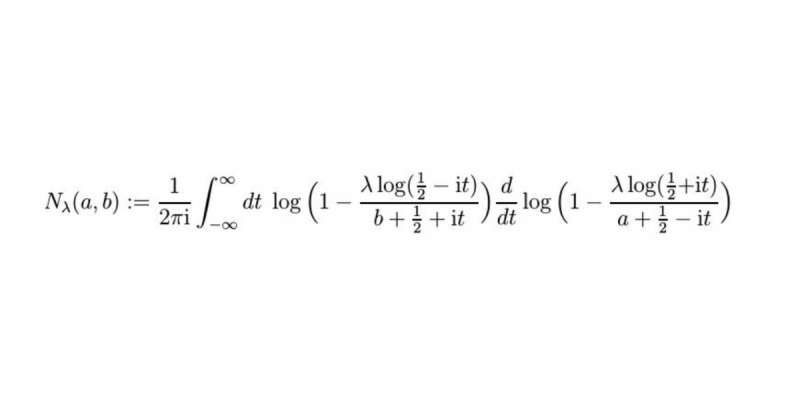
… before you got back to work.
Yes. The next day I succeeded in reducing part of the equation to a simple series of derivatives. Initially, the rest seemed to be difficult. Not until late in the evening did I hit upon the idea of using the Cauchy formula to solve it. I set my alarm clock for 5:30 the next morning and tried it out straight away. It worked at the first attempt, and in the next step I hit upon a formula I had often seen. I knew it would be solved by using the Lambert W function. A few minutes later I got an email from Erik Panzer: he too had thought of the Lambert function, but by a completely different route. As a result, we achieved something which had not been feasible for 10 years: the solution of the integral equation which describes the model of a quantum field theory. It was just incredible.
You use ideas and methods developed by mathematicians in the 18th century which have been almost completely forgotten nowadays.
These old formulae helped us a lot. The Lambert W function, which is an elementary part of our solution, is named after the Swiss mathematician Johann Heinrich Lambert. This equation turns up in a great number of entirely different questions. Due to a lack of awareness of Lambert's groundwork, the Lambert function was invented again and again, and it was only established as a standard in 1993. We also used the Lagrange-Bürmann formula, which helped us to solve an integral with the aid of the Lambert function, as well as the Cauchy formula. In general, mathematics has a lot of respect for its forefathers. Names such as Euler, Lambert, Lagrange, Cauchy, Gauss and Hilbert are cited with the greatest recognition for their achievements. But there are two modern tools I wouldn't want to be without: Wikipedia and computer algebra. You can find comprehensive information on Wikipedia covering well-known – and less well-known – mathematical structures and functions. Computers can solve equations incomparably faster than by hand, and without making any errors
What are the next steps?
A new function occurs in our solution which we have named the Nielsen function. When we have understood it better and have worked out for example how it relates to other known functions, we will submit our work – which is freely accessible online as a pre-print – for publication in a specialist journal with peer reviews.
After that I would like to continue some work I have been engaged on since 2002 with my colleague Prof. Harald Grosse from Vienna. It deals with a quantum field theory for mathematical particles. We will now be able to fully understand this model with the aid of the equation we have solved.
More information: Lambert-W solves the noncommutative Φ4-model. arxiv.org/abs/1807.02945
Provided by University of Münster
















