March 12, 2018 feature
Surprising preference for simplicity found in common model
Researchers have discovered that input-output maps, which are widely used throughout science and engineering to model systems ranging from physics to finance, are strongly biased toward producing simple outputs. The results are surprising, as naïvely there is no reason to suspect that one output should be more likely than any other.
The researchers, Kamaludin Dingle, Chico Q. Camargo, and Ard A. Louis, at the University of Oxford and at the Gulf University for Science and Technology, have published a paper on their results in a recent issue of Nature Communications.
"The greatest significance of our work is our prediction that simplicity bias—that simple outputs are exponentially more likely to be generated than complex outputs are—holds for a wide variety of systems in science and engineering," Louis told Phys.org. "The simplicity bias implies that, for a system made of many different interacting parts—say, a circuit with many components, a network with many chemical reactions, etc.—most combinations of parameters and inputs should result in simple behavior."
The work draws from the field of algorithmic information theory (AIT), which deals with the connections between computer science and information theory. One important result of AIT is the coding theorem. According to this theorem, when a universal Turing machine (an abstract computing device that can compute any function) is given a random input, simple outputs have an exponentially higher probability of being generated than complex outputs. As the researchers explain, this result is completely at odds with the naïve expectation that all outputs are equally likely.
Despite these intriguing findings, so far the coding theorem has rarely been applied to any real-world systems. This is because the theorem has only been formulated in a very abstract way, and one of its key components—a complexity measure called the Kolmogorov complexity—is uncomputable.
"The coding theorem of Solomonoff and Levin is a remarkable result that should really be much more widely known," Louis said. "It predicts that low-complexity outputs are exponentially more likely to be generated by a universal Turing machine (UTM) than high-complexity outputs are. Since anything that is computable can be computed on a UTM, that is a pretty amazing prediction!
"However, the coding theorem has remained obscure because UTMs are rather abstract, because it can only be proven to hold in the asymptotic limit of large complexities, and because the Kolmogorov measure used to determine complexity is fundamentally uncomputable. Our work circumvents these problems using a slightly weaker version of the coding theorem that is much easier to apply."
In the new, weaker version of the coding theorem, the researchers replaced the Kolmogorov complexity with an approximation complexity, which is computable, while still preserving the exponential preference for simplicity. The weaker coding theorem can be readily applied to make predictions regarding practical systems.
"We use the language of input-output maps, which may sound rather abstract," Louis said. "However, many systems studied in science and engineering convert some kind of input to some kind of output through an algorithm. For example, the information encoded in the DNA of an organism (its genotype) could be seen as input, while the organism's characteristics and behavior (its phenotype) could be seen as the output. In a set of differential equations, the input is the parameters of the equations, and the output is the solution of those equations, given some boundary conditions.
"We argue that if you randomly chose input parameters, then such systems are exponentially more likely to produce simple outputs over complex outputs. Since this prediction holds for a wide range of maps, we are making a broad claim. But that's one of its strengths. Our derivation does not require knowing much about how the map (or the algorithm) in question actually works.
"So the main significance of our work is that our weaker version of the coding theorem approximately maintains the exponential bias towards simplicity of the original coding theorem, but is much easier to apply in practice."
One consequence of the results is that it's possible to predict the probability of any particular outcome based on its complexity. Although a simple output is exponentially more likely to appear than a complex output, the researchers note that this does not necessarily mean that simple outputs are more likely to appear than complex outputs in general, since there may be many more complex outputs than simple ones overall.
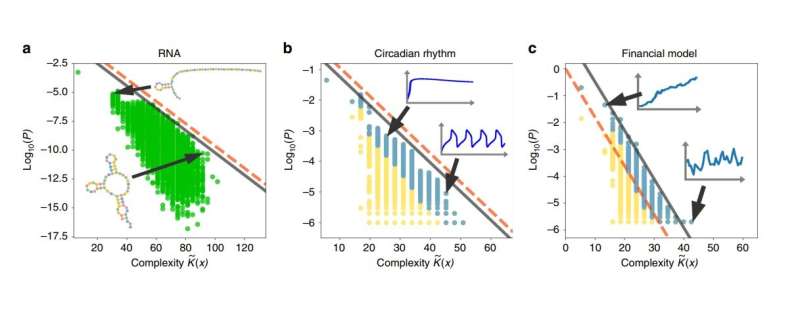
To illustrate a few applications, the researchers used the modified coding theorem to analyze systems of RNA sequences, circadian rhythms, and financial markets, and showed that all of these systems exhibit the simplicity bias. In the future, they also plan to apply the results to computer algorithms, biological evolution, and chaotic systems. However, for a more intuitive explanation of what simplicity bias means, the researchers describe a scenario involving our primate relatives:
"Consider the well-known problem of monkeys typing on a typewriter," Louis said. "If the monkeys type in a truly random way, and the typewriter has N keys, then the probability of getting a particular sequence of length k is just 1/Nk, since there is a 1/N chance of getting the right keystroke at each of the k steps. Thus every sequence of length k is equally likely or unlikely.
"Now consider the case where the monkeys are typing into a computer program. They may then by accident type a short program that generates a long output. For example, there is a 133-character code in the programming language C that correctly generates the first 15,000 digits of π. So instead of 1/N15,000, which is the probability for monkeys getting this right on a typewriter, the odds are much lower, only 1/N133, that the monkeys generate π on the computer.
It turns out that most numbers don't have short programs that generate them, so the best the monkeys on the computer can do for these numbers is to type out a program like 'print number,' which is close the probability that they would get it right on a typewriter anyhow. But for simple outputs, the probability is much higher than for the typewriter. By definition, simple outputs are defined as those which have short programs describing them, and complex outputs are those that can only be described by long programs. So π is, by definition, a number with a low complexity, and therefore it is much more likely to be generated by monkeys typing into a computer program than many other numbers which are not simple.
"What the coding theorem does is to make this intuitive story quantitative. Short programs are more likely to be typed in at random, and since probabilities for length k programs also scale as 1/Nk, simple outputs are exponentially much more likely to appear than complex ones. Our contribution is to demonstrate how to easily calculate the exponential relationship between probability and complexity for many practical systems. What is nice is that you don't need to know much about the map (or equivalently the algorithm) to work out whether an output is likely to appear or not. To a good first approximation, the more compressible an output is, the more likely it is to appear upon random inputs."
More information: Kamaludin Dingle, Chico Q. Camargo, and Ard A. Louis. "Input-output maps are strongly biased towards simple outputs." Nature Communications. DOI: 10.1038/s41467-018-03101-6
Journal information: Nature Communications
© 2018 Phys.org