Mathematicians work to expand their new pictorial mathematical language into other areas
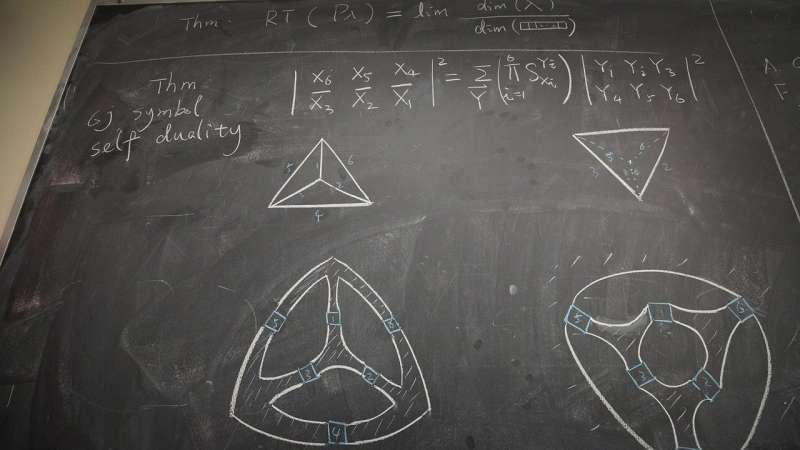
A picture is worth 1,000 words, the saying goes, but a group of Harvard-based scientists is hoping that it may also be worth the same number of equations.
Pictorial laws appear to unify ideas from disparate, interdisciplinary fields of knowledge, linking them beautifully like elements of a da Vinci painting. The group is working to expand the pictorial mathematical language first outlined last year by Arthur Jaffe, the Landon T. Clay Professor of Mathematics and Theoretical Science, and postdoctoral fellow Zhengwei Liu.
"There is one word you can take away from this: excitement," Jaffe said. "And that's because we're not trying just to solve a problem here or there, but we are trying to develop a new way to think about mathematics, through developing and using different mathematical languages based on pictures in two, three, and more dimensions."
Last year they created a 3-D language called quon, which they used to understand concepts related to quantum information theory. Now, new research has offered tantalizing hints that quon could offer insights into a host of other areas in mathematics, from algebra to Fourier analysis, as well as in theoretical physics, from statistical physics to string theory. The researchers describe their vision of the project in a paper that appeared Jan. 2 in the journal Proceedings of the National Academy of Sciences.
"There has been a great deal of evolution in this work over the past year, and we think this is the tip of the iceberg," Jaffe said. "We've discovered that the ideas we used for quantum information are relevant to a much broader spectrum of subjects. We are very grateful to have received a grant from the Templeton Religion Trust that enabled us to assemble a team of researchers last summer to pursue this project further, including undergraduates, graduate students, and postdocs, as well as senior collaborators at other institutions."
The core team involves distinguished mathematicians such as Adrian Ocneanu, a visiting professor this year at Harvard, Vaughan Jones, and Alina Vdovina. As important are rising stars who have come to Harvard from around the world, including Jinsong Wu from the Harbin Institute of Technology and William Norledge, a recent graduate from the University of Newcastle. Also involved are students such as Alex Wozniakowski, one of the original members of the project and now a student at Nanyang Technological University in Singapore, visiting graduate students Kaifeng Bu from Zhejiang University in Hangzhou, China, Weichen Gu and Boqing Xue from the Chinese Academy of Sciences in Beijing, Harvard graduate student Sruthi Narayanan, and Chase Bendarz, an undergraduate at Northwestern University and Harvard.
While images have been used in mathematics since ancient times, Jaffe and colleagues believe that the team's approach, which involves applying pictures to math generally and using images to explore the connections between math and subjects such as physics and cognitive science, may mark the emergence of a new field.
Among the sort of problems the team has already been able to solve, Liu said, is a pictorial way to think about Fourier analysis.
"We developed this, motivated by several ideas from Ocneanu," he said. "Immediately, we used this to give new insights into quantum information. But we also found that we could prove an elaborate algebraic identity for formula 6j-symbols," a standard tool in representation theory, in theoretical physics, and in chemistry.
That identity had been found in an elementary case, but Harvard mathematician Shamil Shakirov conjectured that it was true in a general form. The group has now posted a proof on arXiv.org that is under review for publication later in the year. Another very general family of identities that the group has understood simply using the geometric Fourier transform is known as the Verlinde fusion formulas.
"By looking at the mathematical analysis of pictures, we also found some really unexpected new inequalities. They generalize the famous uncertainty principles of [Werner] Heisenberg and of [G.H.] Hardy and become parts of a larger story," Liu said. "So the mathematics of the picture languages themselves is quite interesting to understand. We then see their implications on other topics."
"I am very taken by this project, because before this, I was working on quantum information, but the only way I knew to do that was using linear algebra," said Bu. "But working with Arthur and Zhengwei, we've been able to use this pictorial language to derive new ideas and geometric tools that we can use to develop new quantum protocols. They have already been useful, and we foresee that these ideas could have wide-ranging applications in the future.
"It's amazing, I think, that we can use a simple pictorial language to describe very complicated algebra equations," Bu continued. "I think this is not only a new approach, but a new field for mathematics."
Ocneanu interjected, "Ultimately what higher-dimensional picture language does is to translate the structure of space into mathematics in a natural way."
Whereas traditional, linear algebra flattens 3-D concepts into a single line of equations, he said, the picture language allows scientists to use 3-D and higher-dimensional spaces to translate the world around them.
"Space, or more generally space-time, is a kind of computational machine," said Ocneanu. "We should really translate what space is doing into the kinds of things mathematicians use, so we can read the structure of space."
For Norledge, the new mathematical language is striking in the way it builds from a handful of relatively simple concepts into a complex theory.
"My background is in representation theory; my thesis is in this area of math called geometric group theory," he said. "So with a background of using pictures and geometric objects, it helps to apply mathematics in this way. We're still trying to realize this, but if this all goes through and succeeds, you've got a very beautiful area of mathematics where you start with just a few axioms, and just from that beginning you can generalize this highly nontrivial theory with this beautiful structure."
"We hope that eventually one can implement the ideas we are studying in new theoretical-physics models, as well as in some practical terms," Jaffe said. "To share in our excitement, take a look at our website."
More information: Arthur M. Jaffe et al. Mathematical picture language program, Proceedings of the National Academy of Sciences (2017). DOI: 10.1073/pnas.1710707114
Journal information: Proceedings of the National Academy of Sciences
Provided by Harvard University