New mathematical framework establishes the risk of dramatic collapses of real networks
A theoretical framework explaining the risk of rare events causing major disruptions in complex networks, such as a blackout in a power grid, has been proposed by a mathematician at Queen Mary University of London.
Rare events can abruptly dismantle a network with much more severe consequences than usual and understanding their probability is essential in reducing the chances of them happening.
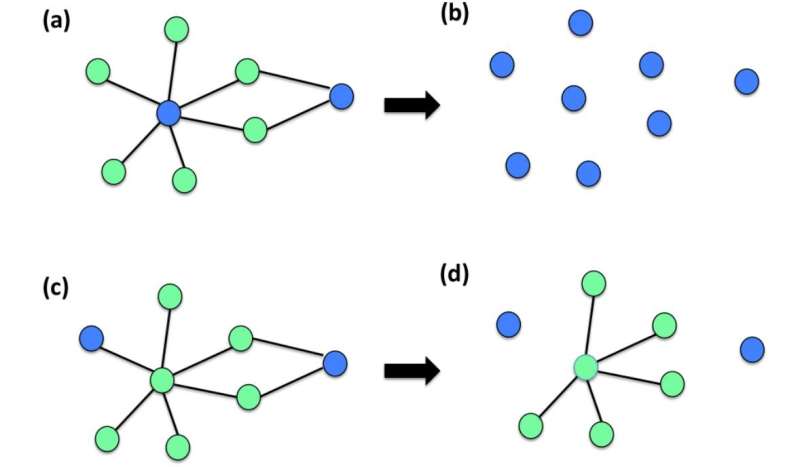
A network is formed by a set of nodes and the links between them. For instance power grids are networks whose nodes are power stations connected by the electrical grid. Similarly an ecological network, which the framework could be applied to, is formed by species connected by ecological interactions like a predator-prey relationship.
Usually if some of the nodes are damaged, networks like these are robust enough to remain functional but on rare occasions specific damage can lead to the dismantling of the whole network and cause major blackouts or ecological regime shifts, such as an ecological collapse.
Mathematicians often use percolation theory, a well-developed branch of applied mathematics that studies the response of a network to the damage of a random fraction of its nodes, to shed light on these phenomena. However, this theory is able only to characterise the average response of a network to random damage. Therefore the prediction of the average behaviour cannot be used to estimate the risk of a network collapse as a result of a rare event.
This study establishes a large deviation theory of percolation that characterises the response of a network to rare events. The proposed theoretical framework correctly captures the effect of rare damage configurations that can be observed in real networks. Interestingly the work reveals that discontinuous percolation transitions - abrupt collapses of a network - are occurring as soon as rare events are taken into consideration.
The theoretical framework could enable strategies to be developed to sustain networks by identifying which nodes need to be preserved to prevent a collapse.
Ginestra Bianconi, author of the study, said: "There is an urgent need to evaluate the risk of collapse in response to rare configurations of initial damage. This result sheds light on the hidden fragility of networks and their risk of a sudden collapse and could be especially useful for understanding mechanisms to avoid the catastrophic dismantling of real networks."
She added: "It is important to estimate the risk of a dramatic cascade of failures because you want to reduce the risk. In the design of a power-grid that must provide the energy to an entire country you want to avoid rare events in which you have major blackouts, or in the design of preservation strategies of an ecosystem that is currently diversified and prosperous you want to know what is the probability of a sudden ecological collapse and mass extinction. Therefore it is necessary to understand this risk of these events happening."
The present large deviation study of percolation considers exclusively node percolation on single networks like those mentioned. However, Ginestra Bianconi suggests the outlined methodology could be extended to the study of more detailed models of propagation of event failures.
More information: Ginestra Bianconi. Rare events and discontinuous percolation transitions, Physical Review E (2018). DOI: 10.1103/PhysRevE.97.022314
Journal information: Physical Review E
Provided by Queen Mary, University of London