Mathematicians develop model for how new ideas emerge
Researchers from Queen Mary University of London have developed a mathematical model for the emergence of innovations.
Studying creative processes and understanding how innovations arise and how novelties can trigger further discoveries could lead to effective interventions to nurture the success and sustainable growth of society.
Empirical findings have shown that the way in which novelties are discovered follows similar patterns in a variety of different contexts including science, arts, and technology.
The study, published in Physical Review Letters, introduces a new mathematical framework that correctly reproduces the rate at which novelties emerge in real systems, known as Heaps' law, and can explain why discoveries are strongly correlated and often come in clusters.
It does this by translating the theory of the 'adjacent possible', initially formulated by Stuart Kauffman in the context of biological systems, into the language of complex networks. The adjacent possible is the set of all novel opportunities that open up when a new discovery is made. Networks have emerged as a powerful way to both investigate real world systems, by capturing the essential relations between the components, and to model the hidden structure behind many complex social phenomena.
In this work, networks are used to model the underlying space of relations among concepts.
Lead author Professor Vito Latora, from Queen Mary's School of Mathematical Sciences, said: "This research opens up new directions for the modelling of innovation, together with a new framework that could become important in the investigation of technological, biological, artistic, and commercial systems."
He added: "Studying the processes through which innovations arise can help understanding the main ingredients behind a winning idea, a breakthrough technology or a successful commercial activity, and is fundamental to devise effective data-informed decisions, strategies, and interventions to nurture the success and sustainable growth of our society."
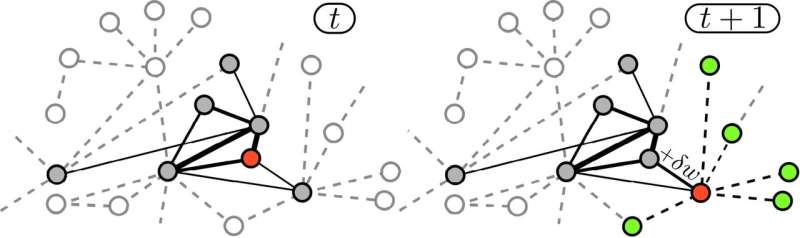
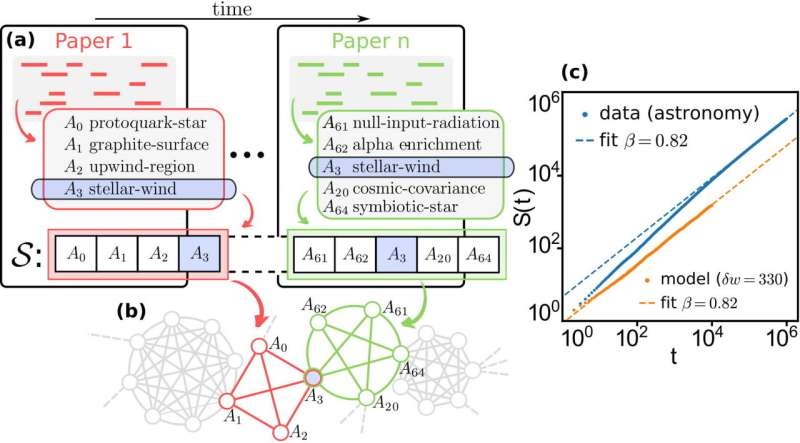
In the study, the discovery process is modelled as a particular class of random walks, named 'reinforced' walks, on an underlying network of relations among concepts and ideas. An innovation corresponds to the first visit of a site of the network, and every time a walker moves from a concept to another, such association (an edge in the network) is reinforced so that it will be used more frequently in the future. The researchers named this the 'edge-reinforced random walk' model.
To show how the model works in a real case, they also constructed a dataset of 20 years of scientific publications in different disciplines, such as astronomy, ecology, economics and mathematics to analyse the appearance of new concepts. This showed that, despite its simplicity, the edge-reinforced random walk model is able to reproduce how knowledge grows in modern science.
Professor Vito Latora added: "The framework we present constitutes a new approach for the study of discovery processes, in particular those for which the underlying network can be directly reconstructed from empirical data, for example users listening to music over a similarity network between songs. We are already working on this idea, together with an extended version of our model, where we study the collective exploration of these networked spaces by considering multiple walkers at the same time."
More information: Iacopo Iacopini et al. Network Dynamics of Innovation Processes, Physical Review Letters (2018). DOI: 10.1103/PhysRevLett.120.048301
Journal information: Physical Review Letters
Provided by Queen Mary, University of London