Researchers devise method to study network resistance to random failures based on 'random walks'

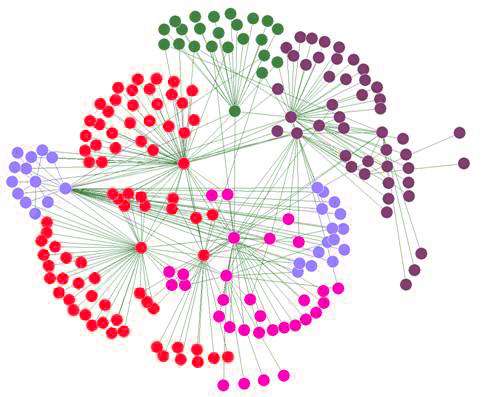
(Phys.org) —A small team of mathematicians with Universitat Rovira i Virgili in Spain, has come up with a way to study a network's resistance to failure. In their paper published in Proceedings of the National Academy of Sciences, the researchers describe the concept of "random walks" and how it can be used to mathematically analyze a wide variety of networks to study its resistance to failure.

We humans have a tendency to build networks—from gas pipelines, to our highway systems to the Internet, networks carry both real world things and virtual information—all necessary for the smooth running of modern economies. Unfortunately, as we learn when the electric grid fails or traffic snarls on the freeway, networks have a tendency to fail us at times. Most people understand intuitively that such failures generaly come about due to a failure in a single part of the network—a car crash, a leak in a pipe or an injury to a body part. Most are aware also of backups put in place to deal with such failures—busses can be used when a metro network suffers a failure or snail-mail can be used if the Internet goes down. But how much redundancy is necessary to keep a network running, and how well does it do so? These are questions scientists and engineers grapple with every day. In this new effort, the team in Spain has developed a new tool to help, they call it the concept of "random walks."

To explain their idea, they used London's mass transit system—the Tube—as their basic network. What happens when a section of the system goes down, they asked. Because people are in the middle of it, there is no clear direction on what to do, i.e. to get to where they want to go. Some use logic, mapping out the rest of the network in their head. Others, however, simply begin walking in a random direction, assuming that a solution will reveal itself. In multi-layer networks (where there are parts that are separate from each other) it turns out, people taking random walks works out pretty well. The researchers came to this conclusion by applying mathematical algorithms to the idea and then creating models based on them. They found that random walks can be programmed into virtually any network model and doing so helps to demonstrate the robustness of the network as well how well it will operate when failures do occur. Thus, new networks can be put to the test before they are constructed, making them work better in the long run.

© 2014 Phys.org