Mathematicians crack 44-year-old problem
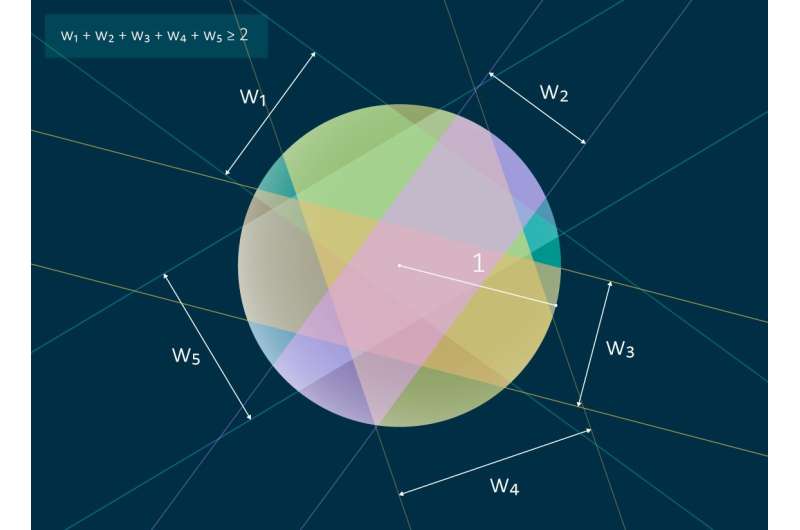
Israel Institute of Technology and Alexandr Polyanskii from the Moscow Institute of Physics and Technology (MIPT) have proved László Fejes Tóth's zone conjecture. Formulated in 1973, it says that if a unit sphere is completely covered by several zones, their combined width is at least π. The proof, published in the journal Geometric and Functional Analysis, is important for discrete geometry and enables mathematicians to formulate new problems.
Discrete geometry studies the combinatorial properties of points, lines, circles, polygons and other geometric objects. What is the largest number of equally sized balls that can fit around another ball of the same size? What is the densest way to pack equally sized circles in a plane, or balls in a containing space? These questions and others are addressed by discrete geometry.
Solutions to problems like these have practical applications. Thus, the dense packing problem has helped optimize coding and correct mistakes in data transmission. A further example is the four-color theorem, which says that four colors suffice to plot any map on a sphere so that no two adjacent regions have the same color. It has prompted mathematicians to introduce concepts important for graph theory, which is crucial for many of the recent developments in chemistry, biology and computer science, as well as logistics systems.
Tóth's zone conjecture is closely related to a number of other problems in discrete geometry that were solved in the 20th century dealing with covering a surface with strips. The first among them was the so-called plank problem, which involved covering a disk with strips bounded by parallel lines. Alfred Tarski and Henryk Moese offered a simple proof showing that the combined width of these strips, or planks, cannot exceed the diameter of the disk. That is, there is no better way to cover a disk than with a single plank whose width equals the disk's diameter. Thøger Bang then solved the problem on covering an arbitrary convex body with strips. Namely, he proved that the combined width of the strips covering a convex body is at least the width of the body itself, that is, the minimum width of a single strip covering the body.
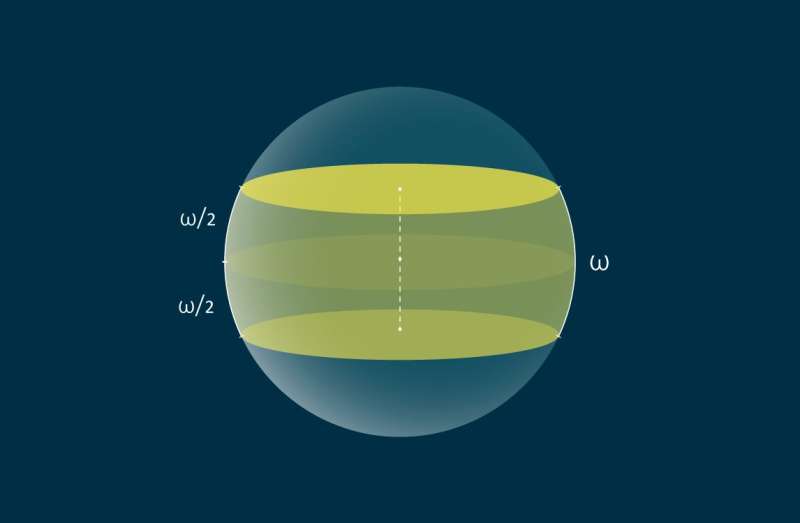
The problem tackled by the authors is different in that it involves covering a unit sphere with specially constructed zones. Specifically, each zone is the intersection of the sphere with a certain three-dimensional plank, where a plank is the region of space contained between two parallel planes that are symmetric with respect to the center of the sphere. Alternatively, zones can be defined in geodesic metric space without recourse to planks: A zone of width ω on the surface of a unit sphere is the set of points that lie no farther than ω/2 from the great circle, or equator, with the distances between points measured as the shortest arcs connecting them. The mathematicians had to find the minimum combined width of such zones covering the unit sphere. Thus, the problem differs from those previously solved in how width is measured—it is defined as the length of an arc, rather than the Euclidean distance between parallel lines or planes.
The proof presented by Jiang and Polyanskii was inspired by Bang, who solved the problem on covering a body with strips by forming a special finite set of points within the body, one of which was supposedly not covered by any of the strips. In a way, both Bang and the authors produce a proof by contradiction. In the case of Fejes Tóth's conjecture, the mathematicians hypothesized that the combined width of zones completely covering the sphere was less than π and sought to arrive at a contradiction—namely, find a point lying on the sphere but not in any of the zones.
The authors have shown that it is possible to form a set of points in three-dimensional space so that at least one point is not covered by the planks constituting the zones. If this whole set lies inside the sphere, it is then relatively easy to plot another point on the sphere that is also not covered by the planks, and hence by the zones. If any of the points in the set happens to lie outside the sphere, it turns out to be possible to substitute one larger zone for several smaller ones, whose combined width is equal to that of the larger zone. Thus, it is possible to reduce the number of zones in the initial problem without affecting their combined width. Eventually, a point on the sphere is identified that is not covered by the zones. This runs counter to the hypothesis that the combined width of the zones is less than π, proving Fejes Tóth's conjecture.

The problem was solved in n-dimensional space, but the authors say this makes it no different from the case with three dimensions.
"Fejes Tóth's problem has fascinated mathematicians in the field of discrete geometry for over 40 years," says author Alexandr Polyanskii of the Department of Discrete Mathematics, MIPT. "This problem turned out to have an elegant solution, which we were fortunate to find. Fejes Tóth's problem prompted us to consider another, more fundamental conjecture on the covering of a sphere by shifted zones defined as the intersection of the sphere with three-dimensional planks that are not necessarily centrally symmetric."
More information: Zilin Jiang et al, Proof of László Fejes Tóth's zone conjecture, Geometric and Functional Analysis (2017). DOI: 10.1007/s00039-017-0427-6
Provided by Moscow Institute of Physics and Technology