February 19, 2016 report
Physicists discover easy way to measure entanglement—on a sphere
(Phys.org)—Quantum entanglement—which occurs when two or more particles are correlated in such a way that they can influence each other even across large distances—is not an all-or-nothing phenomenon, but occurs in various degrees. The more a quantum state is entangled with its partner, the better the states will perform in quantum information applications. Unfortunately, quantifying entanglement is a difficult process involving complex optimization problems that give even physicists headaches.
Now in a new paper to be published in Physical Review Letters, mathematical physicists Bartosz Regula and Gerardo Adesso at The University of Nottingham have greatly simplified the problem of measuring entanglement.
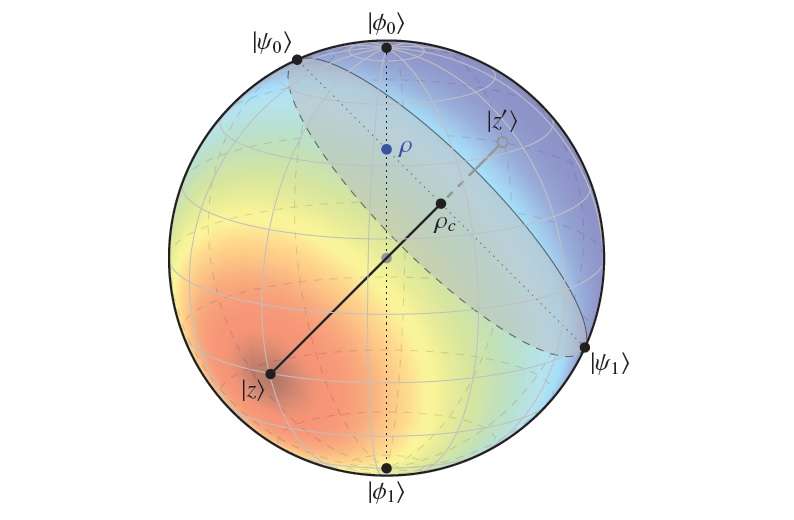
To do this, the scientists turned the difficult analytical problem into an easy geometrical one. They showed that, in many cases, the amount of entanglement between states corresponds to the distance between two points on a Bloch sphere, which is basically a normal 3D sphere that physicists use to model quantum states.
As the scientists explain, the traditionally difficult part of the math problem is that it requires finding the optimal decomposition of mixed states into pure states. The geometrical approach completely eliminates this requirement by reducing the many possible ways that states could decompose down to a single point on the sphere at which there is zero entanglement. The approach requires that there be only one such point, or "root," of zero entanglement, prompting the physicists to describe the method as "one root to rule them all."
The scientists explain that the "one root" property is common among quantum states and can be easily verified, transforming a formidable math problem into one that is trivially easy. They demonstrated that the new approach works for many types of two-, three- and four-qubit entangled states.
"This method reveals an intriguing and previously unexplored connection between the quantum features of a state and classical geometry, allowing all one-root states to enjoy a convenient visual representation which considerably simplifies the study and understanding of their properties," the researchers explained.
The simple way of measuring a state's entanglement could have applications in many technological areas, such as quantum cryptography, computation, and communication. It could also provide insight into understanding the foundations of thermodynamics, condensed matter physics, and biology.
More information: Bartosz Regula and Gerardo Adesso. "Entanglement quantification made easy: Polynomial measures invariant under convex decomposition." Physical Review Letters. DOI: 10.1103/PhysRevLett.116.070504, arXiv:1512.03326 [quant-ph]
Journal information: Physical Review Letters
© 2016 Phys.org