Topology looks for the patterns inside big data

Big data gets much attention from media, industry and government. Companies and labs generate massive amounts of data associated with everything from weather to cell phone usage to medical records, and each data set may involve hundreds of variables.
These sets are so large and complex that traditional methods of looking for patterns within them can't make much headway. Often touted as a silver bullet, data analytics certainly have the potential to make inroads into once intractable problems. But we have to be able to figure out what we're looking at.
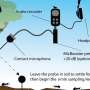
Statistics 101 invariably contains a lecture or two about linear regression – finding the best line that fits a set of points scattered in a plane. These graphs often show up in articles about climate change, for example, where temperature and other weather data are plotted against time, or in economic forecasts where employment or GDP history is used to extrapolate into the future.
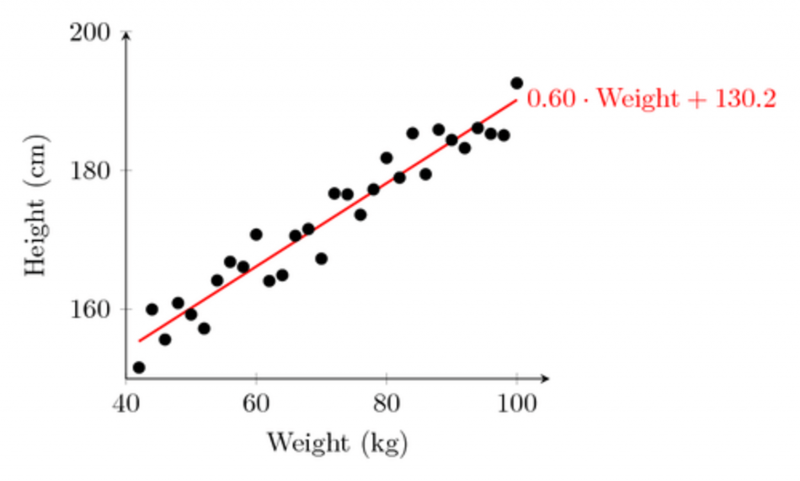
But what if the set of points doesn't lie near a line but instead forms something like a circle?
Clearly regression isn't useful in this context, but we know that only because we can see that the points form a circle.
Now imagine instead a collection of points lying on a circle in a higher-dimensional space. In three dimensions we might be able to see the circle, but if we have more variables, as often happens when examining large data sets, we are in trouble. How could we detect the circle? Better: how could we tell a computer to find the circle?
These are the types of questions arising from the growth of big data – and algebraic topology provides some answers.
How to make sense of big data spatially
Topology is sometimes called "rubber sheet geometry." To a topologist, a sphere and a cube are the same thing. Imagine a cube made from flexible material; inserting a straw and blowing into the cube would puff it out into a sphere. Operations like this are called deformations, and two objects are considered to be the same if one can be deformed to the other.
Topologists study spaces by assigning algebraic objects called invariants to them. They may be as simple as an integer, but they are often more complicated algebraic structures. For data analysis, the invariant of choice is persistent homology.
Ordinary homology measures the number of "holes" that cannot be filled in a space. Let's think about a sphere again. If we draw a loop on the sphere, it bounds a 2-dimensional disc on the surface; that is, we can fill in any loop on the sphere and so there are no 2-dimensional "holes." By contrast, the surface of the sphere itself bounds a 3-dimensional "hole" that cannot be filled.
The Betti numbers of a space count the number of such unfillable holes of each dimension. A sphere has second Betti number equal to 1 (because its interior cannot be filled) and first Betti number equal to 0 (because any loop bounds a disc on the sphere). The zero-th Betti number counts the number of pieces a space has; in the case of the sphere we have one piece. There are higher-dimensional versions of this as well for more complicated spaces.
The problem with using ordinary homology for data analysis is that if we compute the homology of a discrete set of data points, we will be disappointed. There are no holes, only a collection of disconnected points. The zero-th Betti number will count how many points there are, but as there are no loops or spheres in such a set the higher Betti numbers will all be 0. This is where persistent homology enters the story.
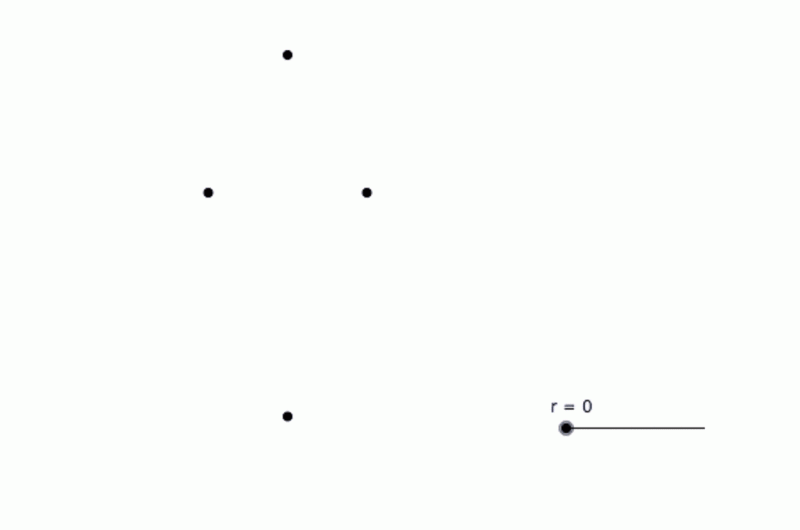
We need to take our discrete set of points and join them together. Imagine putting a small ball of radius r around each point in our data set. If r is very small, then none of the balls will intersect and the Betti numbers of all the balls in the set are the same as for the discrete set.
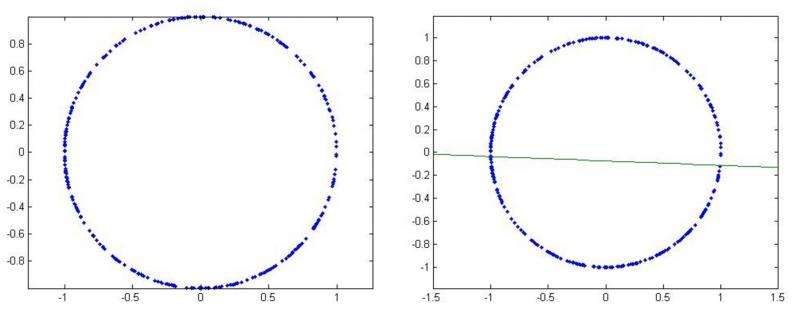
However, if we allow r to grow, then eventually the balls will begin to touch and we will likely get nontrivial higher Betti numbers. In the animation, we see that once r reaches a certain threshold, the balls around the top three points intersect in pairs and therefore contain the triangle joining the three points. Moreover, we cannot fill in the triangle since there's a small gap in the middle; this means the first Betti number is 1 at that stage. But as r gets a bit bigger, then all three balls intersect at once and we can fill in the triangle; the first Betti number then drops to 0.
Persistent homology tracks these numbers as the radius grows; the plot of these numbers against the parameter r is called a barcode. Long bars suggest features in the data that may be significant (they persist, hence the terminology). Short bars often arise from noise in the data and may be disregarded (or not – context is important).
So what we've done is pass from a discrete collection of points to a sequence of more complicated spaces (one for each r) which hopefully model the data much better than a simple linear regression might.
In the above animation, we show how a few points on a circle might be modeled in this way. We have suppressed the balls around the points, connecting two points when their associated balls overlap, forming triangles when three intersect and so on. A circle persists for quite a long time, leading us to guess that our data lie near a circle.
Applications beyond the theory
Gunnar Carlsson of Stanford University is one of the pioneers of topological data analysis. One of his group's first successes was the discovery of the topology of the space of natural images. This data set consists of several million 3-pixel by 3-pixel patches sampled from black and white digital photographs. Each pixel is described by a number between 0 and 255, measuring its grayscale value; each 3-by-3 patch then corresponds to a point in a 9-dimensional space, each coordinate giving the numerical value of the associated pixel. After tossing out the constant patches and doing some normalizations, this space lies inside a 7-dimensional sphere. At first glance, the set appears to fill out the sphere, but structure emerges by restricting attention to areas where the points pack closer together.
Carlsson and his collaborators showed that the data actually lie on a Klein bottle, a nonorientable 2-dimensional surface embedded in the sphere. They were able to push this further to find a compression algorithm for photos that is slightly better than the industry standard JPEG 2000. Carlsson has published an excellent survey of this work.
In light of this success, Carlsson and some of his colleagues founded AYASDI, a company with a growing roster of clients in banking, finance, government and other industries. They use these and other techniques to analyze diabetes, breast cancer and cardiopulmonary disease data. The results are encouraging – certain subgroups of patients with high survival rates, invisible using traditional statistical methods, may be found via these techniques.
The real promise of these methods, however, lies in the possibility of tailoring treatments and solutions to individuals. Analysis of large data sets lets us know, for example, that a drug once thought to be 80% effective is actually 100% effective on 80% of patients, identifiable via some marker. Topological data analysis provides another tool to advance these analytics, often identifying features that were hidden before.
Source: The Conversation
This story is published courtesy of The Conversation (under Creative Commons-Attribution/No derivatives).
![]()