Quantum computing—breaking through the 49 qubit simulation barrier
Quantum computing is at the threshold of tackling important problems that cannot be efficiently or practically computed by other, more classical means. Getting past this threshold will require us to build, test and operate reliable quantum computers with 50 or more qubits.
Achieving this potential will require major leaps forward in both science and engineering. To help make those leaps, methods are needed to test quantum devices and to compare observed behaviors with desired behaviors so that the design, manufacturing, and operation of these devices can be improved over time. In particular, to test whether the measured outcomes observed on a quantum device are consistent with the quantum circuit being executed, one needs the ability to compute expected quantum amplitudes (complex numbers used to describe the behavior of systems) for those outcomes in order to test arbitrary circuits. Quantum circuits can be thought of as sets of instructions (gates) that are sent to quantum devices to perform computations.
That need presented us with a problem. At roughly 50 qubits, existing methods for calculating quantum amplitudes require either too much computation to be practical, or more memory than is available on any existing supercomputer, or both. IBM Research put together a team this year to study this problem, targeting short-depth circuits for systems of 49 qubits and beyond. We have published our approach to solving this problem to arXiv: arxiv.org/abs/1710.05867.
I was part of this team and came up with a key idea at a seemingly inconsequential moment.
Visualizing quantum gates as a bristle brush
A qubit, or quantum bit, is the basic unit of information in quantum computing, just as a bit is in classical computing. A qubit, however, can represent both 0 and 1 simultaneously – in fact, in weighted combinations (for example, 37%-0, 63%-1). Two qubits can represent four values simultaneously: 00, 01, 10, and 11, again in weighted combinations. Similarly, three qubits can represent 2^3, or eight values simultaneously: 000, 001, 010, 011, 100, 101, 110, 111. Fifty qubits can represent over one quadrillion values simultaneously, and 100 qubits over one quadrillion squared.
When qubits are measured, their quantum states collapse to only one of these represented values, where the weights of the values – the quantum amplitudes – define the probabilities of observing those values. The great promise of quantum computing is the potential to perform parallel computations over exponentially many possible outcomes, to yield quantum states where the desired results of computations have large amplitudes and, hence, will be observed with high probability when qubits are measured.
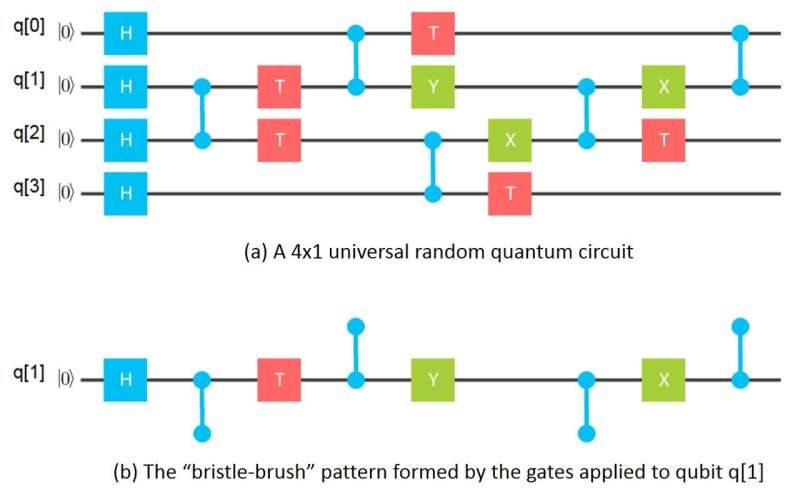
My seemingly inconsequential moment came one night while washing dishes and using a bristle brush to clean a tall glass. It suddenly occurred to me that if one looks at the gates applied to a given qubit in a grid circuit, the gates form a bristle-brush pattern where the bristles are the entangling gates that are being applied to that qubit. Mathematically, that "bristle brush" of gates corresponds to a tensor and the bristles to tensor indices. A tensor in mathematics essentially corresponds to an n-dimensional array in computer science.
That insight immediately led to the idea of pulling a grid circuit apart into individual "bristle brushes," one for each qubit, then computing the corresponding tensors, and finally combining the tensors for each qubit to calculate the quantum amplitudes for the overall circuit. By the next morning I had figured out how to calculate amplitudes for a 64–qubit, depth 10 circuit using only one Gigabyte of memory by pulling groups of 16 qubits apart. From there the idea snowballed into more general ways of partitioning circuits into sub–circuits, simulating sub–circuits separately and combining the results of sub-circuits in various orders to calculate desired amplitudes.
The net result is a method for calculating quantum amplitudes that requires orders of magnitude less memory than previous methods while still being comparable to the best of these methods, in terms of the amount of computation performed per amplitude. These smaller memory requirements are achieved using tensor slicing in combination with the insights mentioned above to calculate output amplitudes of circuits in slices, without having to calculate and/or store all amplitudes at once.
When calculating amplitudes for measured outcomes, only those slices that correspond to actual measured outcomes need be calculated. In other words, for the purpose of evaluating the performance of a quantum device based on measured outcomes, a full simulation is not necessary and one does not need to incur computational costs that are exponential in the number of qubits. This is an important benefit of our approach.
However, if one actually is interested in performing full simulations, our slicing method has a further benefit in that slices can be computed completely independently in an embarrassingly-parallel fashion – meaning they can be easily separated – enabling computations to be distributed across a network of loosely-coupled high-performance computing resources. This possibility completely changes the economics of full simulations, enabling quantum circuits to be simulated that were previously thought to be impossible to simulate.
Simulating 49 and 56 qubit circuits using a supercomputer
Our research team reached out to Lawrence Livermore National Laboratory (LLNL) and the University of Illinois to turn this latter possibility into reality. Using the Vulcan supercomputer at LLNL and the Cyclops Tensor Framework originally developed at the University of California, Berkeley to do the tensor manipulations, we first chose to simulate a 49–qubit universal random circuit of depth 27, which has been proposed as a demonstration of so-called quantum supremacy. For this simulation, the calculations were divided into 2^11 slices with 2^38 amplitudes calculated per slice; 4.5 Terabytes were required to hold the tensor values. Slice computations were embarrassingly parallelized across six groups of four racks of processors, where each group of four racks comprised 4,096 processing nodes with a total of 64 Terabytes of memory. Such 49-qubit circuits were previously thought to be impossible to simulate because previous methods would have required eight Petabytes of memory, which exceeds the capacity of existing supercomputers.
For our next demonstration, we chose a 56–qubit universal random circuit of depth 23, which would have been impossible to simulate using previous methods because one Exabyte of memory would have been required. Calculations were divided into 2^19 slices of 2^37 amplitudes each. But in this case we chose to calculate amplitudes for only one arbitrarily selected slice for demonstration purposes; 3.0 Terabytes were required to hold tensor values and computations were performed on two racks of 2,048 processing nodes with a total of 32 Terabytes of memory.
In addition to these demonstrations, we also discovered ways of partitioning the 49-qubit circuit so that only 96 Gigabytes of memory is needed for its simulation, with only slightly more than double the computational requirements. We also discovered a partitioning that requires 162 Gigabytes for which there is barely any increase in computational requirements. The possibility therefore exists to now perform these simulations on clusters of high-end servers, instead of using supercomputers.
Advances in simulation will help advances in quantum hardware
Although the full extent of what is now classically computable using our methods still remains to be determined, it is clear that this advance has enabled us to cross a threshold in the simulation of short–depth quantum circuits of 49 qubits and larger. Pragmatically, the methods will facilitate the testing and understanding of the operation of physical devices. They will also facilitate the development and debugging of short–depth algorithms for problems where quantum computing has the potential to provide real advantage over conventional approaches.
At least for quantum devices now under development or on the drawing boards, the ability to perform these simulations has now become a question of the amount of compute resource that can economically be procured and not whether the simulations can be physically performed at all. For example, in the case of our 56-qubit simulation, a full simulation was not performed simply because our time allocation on Vulcan had run out. There is no question that a full 56-qubit short-depth circuit simulation can now be physically performed. Nor are the run times of these simulations physically limited by the resources available on isolated computer systems. Because slice calculations can be embarrassingly parallelized, they can be distributed across networks of loosely-coupled systems with minimal communication, allowing strong scalablility to be achieved up to the number of slices. Cloud–based quantum simulation may ultimately permit fairly large quantum circuits to be simulated.
Does this mean that we do not need actual quantum computers? Not at all. We absolutely will need them! Depending on the particular kind of application, we will need physical quantum computers to perform computations that will either require too much memory, or too much processing power to be economically performed on classical computers. And, at some point, we truly will have evidence that quantum computers will have an advantage over classical computers for some practical applications, in a very real-world sense.
This is not some artificial notion of "quantum supremacy." Rather, we are now in a period where we are getting quantum-ready to take full advantage of the quantum hardware, software and engineering capabilities that we put online. Simulation is already an integral part of this quantum-ready phase.
IBM has made access to simulators and actual hardware of five and 16 qubits available as part of the IBM Q experience, which provides resources to learn and experiment with. We also have a quantum SDK, or Quantum Information Software Kit (QISKit) to make building circuits easy. To help learn more about how to get started, we have provided Jupyter notebook examples on github.
As device technology advances, we will move into a period of quantum advantage where a broad range of enterprises, scientists and engineers will make full use of the hardware and the power of quantum computing to continue to solve increasingly difficult and complex problems. During this quantum-advantage phase, advanced simulation capabilities will be needed to support both the research and development of new quantum algorithms as well as the advancement of the device technology itself.
More information: Breaking the 49-Qubit Barrier in the Simulation of Quantum Circuits. arxiv.org/abs/1710.05867
Provided by IBM