Correcting errors at the quantum computing scale

Computing power has grown exponentially over many decades, so why is the much-promised next leap of quantum computers taking so long to arrive?
One reason is that the information in a quantum system is sensitive to error-inducing noise in a way that classical information is not. This noise is everywhere and unavoidable, arising from microscopic oscillations of atoms and electrons in all matter. So we have to invent new ways of dealing with quantum errors.
When you make a phone call in a congested network, or scratch a CD, the technology can still work: conversations remain comprehensible and music still plays.
This is because these devices use error correcting codes: even if errors corrupt the raw data stream, the important logical information can still be reconstructed. And these can be adapted for quantum computing.
A time you can count on
To see how this works for classical coding, consider the solution used by early navigators.
They knew that longitude could be calculated from the elevation of the Sun so long as the time at home port was known—hence the naval imperative to build accurate, stable clocks.
Ideally, one clock would be sufficient, but what if something went wrong? Two clocks are better, so long as they both agree. But if they disagree, which is right? With three clocks, a majority vote allows the timekeeper to detect and reset a wayward timepiece.
For binary data, represented by 0s and 1s, repetition protects information: a logical bit "0" is represented in three physical bits as 000, while "1" is represented as 111.
Suppose during data transmission of "0", the last physical bit was accidentally flipped, so that the received message is 001. The recipient would immediately see that an error had corrupted the data.
Further, by taking a majority vote, she would guess that an error affected the third physical bit, and correctly decode the logical bit: "0". As long as errors are rare, the repetition code will allow logical data to be transmitted reliably over a noisy, error-prone channel.
Known unknowns
One quantum wrinkle in this picture is that it involves a "measurement". The receiver knows exactly what physical bits she received (001 in the example, above), which implies that she had to measure them (that is, look at them).
But quantum mechanics tells us that the act of measurement fundamentally changes the state of a quantum system. Simply measuring quantum bits (qubits) changes the message.
So a quantum receiver isn't allowed to measure the qubits directly, but she still needs to figure out whether errors have occurred, and where.
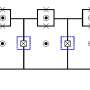
To resolve this we return to the repetition code for guidance. Instead of looking at the bit values, the receiver could instead ask the following two questions:
- Q1: is the first bit the same as the second bit?
- Q2: is the second bit the same as the third bit?
If there were no errors, the answer to both of these questions would be "yes", regardless of whether the message was 000 or 111.
But if the last bit suffered an error (receiving 001 or 110), the answer to Q1 would be "yes" but Q2 would be "no". From this response, the recipient can infer the existence of an error and its location.
Similarly, an error on the first bit will be revealed by the pattern Q1="No", Q2="Yes". An error on the middle bit will be revealed by Q1=Q2="No". Thus, any single error will be uniquely determined by these answers, and can be repaired.
Knowing which physical bit suffered an error, she would fix it by deliberately flipping that bit, to reverse the effect of the original error. This can happen without knowing the state of the damaged bit.
Notice that answering these questions only requires comparative knowledge of the received bits. It does not depend on their particular value, nor the encoded logical information.
This principle captures the essence of quantum error correcting codes. It allows us to simultaneously identify errors and avoid damaging quantum information.
Rather than measuring the value of individual physical qubits, a series of comparative questions are asked: "Are the qubits in group A the same as each other?", "Are the qubits in group B the same as each other?" and so on. The answers to these questions yield clues as to the whereabouts of errors, but without revealing the message itself.
These answers are then used to infer and correct the likely errors.
The logical quantum information is encoded in yet another combination of qubits, which we measure only when we really do want to discover the logical quantum state.
This approach is active, and computationally expensive for large data sets. For some applications, it is necessary. But if engineers in the 1940s had faced a similar struggle to develop early computers, I suspect that the laptop I'm writing this on would never have been built.
Magnetic stability
Instead, they were lucky, as nature itself does classical error correction for free. Magnets are incredibly stable, so they are used to store vast amounts of information in hard disks with almost no active error correction.
Magnets are just collections of many magnetic atoms that tend to align their magnetic axes with one another, so they all point "north".
If a cosmic ray spontaneously kicks the magnetic orientation of one atom, its atomic neighbours exert a magnetic force that realigns it with the majority direction. So a magnet can be thought of as a piece of matter that passively error corrects itself, by a local majority vote.
Unfortunately for quantum computers, we know of no such passively stable state of quantum matter. In fact, we have mathematical proofs that such matter cannot exist in a two-dimensional universe, while it can in a four-dimensional universe.
So far, we don't know whether passively stable quantum matter exists in our own three-dimensional universe.
We do know that with enough skill and resources, we can actively correct quantum errors.
But to build a quantum memory is an ongoing challenge. There is nothing like a "quantum magnet" to easily store quantum information for us. We have to design and build such a system from the ground up, almost literally atom by atom.
One of the first major tasks a quantum computer will do is to perform quantum error correction on itself. Prosaic though this sounds, it will be the first instance in our known universe of truly quantum matter.
Provided by The Conversation
This article was originally published on The Conversation. Read the original article.![]()