August 14, 2017 feature
Trophic coherence explains why networks have few feedback loops and high stability
(Phys.org)—Complexity – defined as having emergent properties or traits that are not a function of, and are therefore difficult or inherently impossible to predict from, the discrete components comprising the system – is a characteristic of complex systems at a wide range of scales (such as genes, neurons and other cells, brains, computers, language, and both natural and sociopolitical ecosystems) that comprise interconnected elements capable of self-modification via feedback loops. At the same time, there are networks (biological and otherwise) that have far fewer of these loops than might be expected – but while these low feedback loop networks are known to be display high stability, the mechanism for feedback suppression (which imparts that stability) has remained unidentified. Recently, however, scientists at University of Warwick and Imperial College London have shown that the level of feedback in complex systems is a function of trophic coherence – a property that reveals the distribution of nodes into high- and low-feedback network levels.
Dr. Samuel Johnson discussed the paper that he and Dr. Nick S. Jones published in Proceedings of the National Academy of Sciences. "Demonstrating that trophic coherence is a property found in a wide range and scale of ecosystems and networks was actually easier than we had expected," Johnson tells Phys.org. "We'd previously identified trophic coherence as an important property of food webs1, in which our main result was the role trophic coherence played in ecosystem stability." (Food webs are ecosystem networks of species trophic levels – that is, what a species eats, and what it is eaten by – and in fact, the word trophic derives from the Greek τροφή (pronounced trophē), which refers to food or nourishment.) "Ecologists have long characterized species in food webs by their trophic levels, so the idea of measuring how well defined these levels were seemed very natural."
However, he points out that while researchers have, over the last 15 or so years, defined and studied a great many quantities associated with complex networks, it appears that the role of trophic levels in networks other than food webs have not been studied. "All we had to do was get the data other researchers have made available for various different kinds of networks, and measure the trophic levels and coherence associated with them, he explains. "Then, when we set about developing a mathematical framework that could relate trophic coherence to other network quantities, one of the first steps was to derive equations for the expected values of trophic coherence and mean trophic levels in random graphs – that is, the values we'd expect a network to have if the edges had been placed randomly between the nodes. This in turn allowed us to investigate a given empirical network and conclude, for instance, whether it was more or less coherent than if it was random."
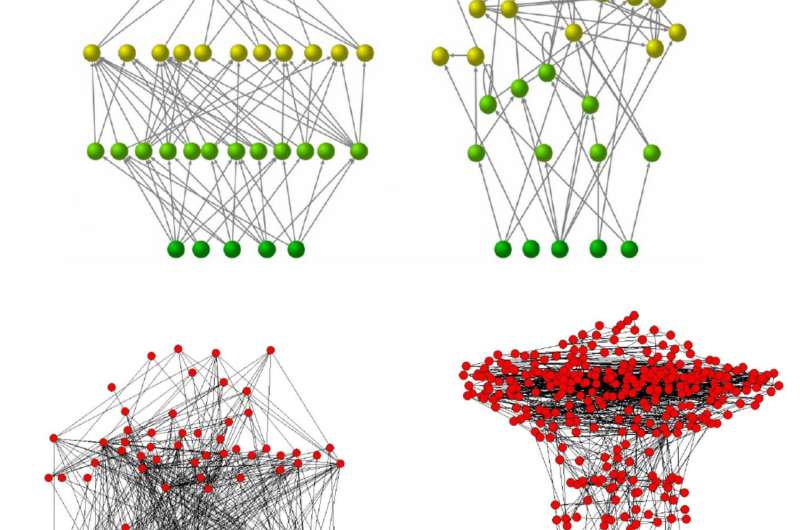
Regarding their derivation of analytic mathematical expressions that show looplessness is a likely consequence of trophic coherence, Johnson recounts, the scientists could see intuitively – or by drawing pictures of networks with greater and lesser coherence – that this property was related to the likely number of cycles (or loops) in directed networks (that is, those in which the links, or edges, have a direction). In order to study this relationship mathematically, he adds, they employed the statistical physics method of ensembles – virtual collections of a large to infinite number of identical systems whose behavior are inferred from the ensemble's aggregate behavior – which has been used to study random graphs.
The scientists credit a moment that proved key to their investigation. "Our crucial insight was that given its trophic coherence, we could associate the expected number of cycles in a network, with the probability that a particular kind of random walker on a line would return to its starting point." Random walkers – imaginary objects whose movement is determined a random selection between two or more choices at each increment, or hop. "Random walkers have proven useful concepts in a wide range of contexts," Johnson notes, "from Albert Einstein's explanation of Brownian motion that proved the existence of molecules, to Sergei Brin and Larry Page's PageRank algorithm that gave rise to Google. In our case, we defined random walkers whose hops were drawn from a distribution centred at one and with standard deviation equal to the network's trophic incoherence." The researchers found that higher incoherence was associated with a higher probability of the walker returning to its origin as well as a higher prevalence of loops in the associated network.
With this method, Johnson tells Phys.org, they were able to obtain expectations and probability distributions for several quantities of interest as a function of trophic coherence, which they termed the coherence ensemble. Moreover, they found that once the trophic coherence was taken into account, the numbers of cycles and related magnitudes measured in all the empirical networks they studied were very close to their theoretical expectations. "From this we were able to conclude that trophic coherence and properties such as looplessness" (which they loosely define as having few or no cycles) "were closely related.
"It could, of course, be the case," Johnson acknowledges, "that certain classes of real networks are coherent as a consequence of some process which suppressed cycles. For instance," he illustrates, "if ecosystems with too many cycles tended to become unstable and collapse, then perhaps only loopless ones survived, and trophic coherence followed from that. However, when we generated networks in a computer so as to have no cycles, we found that this does not induce trophic coherence, while those generated to be sufficiently coherent are loopless." The researchers therefore concluded that coherence-inducing mechanisms are most likely responsible for looplessness in nature.
In addition to the examples of looplessness resulting from trophic coherence mentioned in their paper, Johnson discussed several classes of networks in which trophic levels are likely to be related to some kind of node function, as seems to occur with syntactic function in word adjacency graphs. "We'd expect that if we could obtain data on such systems, we might find that their trophic coherence or incoherence plays a role in their behavior, via its effects on looplessness or loopfulness, as the case may be. More broadly, we believe that classifying the nodes in such networks by trophic level might be useful, as is the case of ecosystems." For example, he illustrates, power relations between people in various kinds of organizations might follow this pattern. "Imagine an army, a corporation, or a whole society, in which each person is a node and a directed edge (aka arrow) points from every individual to those to whom they report, or owe some kind of obedience. A person's trophic level would give an indication of their hierarchical position, and perhaps the trophic coherence of the whole system might be related to the speed of information transmission or its robustness to revolts. This is something we're currently thinking about."
The scientists are also hoping to study the meaning of trophic levels in neural networks. "We included only one example of these in our paper – the much-studied brain of the C. elegans worm – but we're interested in effects on computational abilities, in which feedback loops can be very important. It's curious that neural networks used for deep learning are perfectly coherent – so what might a bit of incoherence do?"
While not discussed in this paper, Johnson and Phys.org discussed the question of whether the number of a system's feedforward loops is affected by trophic coherence. "It's very interesting you should ask that! As part of his doctoral work, Janis Klaise has been looking into this very question – and we have a paper submitted showing that this is indeed the case. It has been known for some time that if one studies the motif profiles of empirical networks – that is, the prevalence of each of the possible ways in which triplets of nodes can be connected – there are several broad families of networks with similar profiles." There are two main groups of food webs, he illustrates, differing primarily in whether the feedforward loop is under- or over-represented, thereby corresponding to more or less trophically coherent food webs, respectively.
![Network of concatenated words from Green Eggs and Ham, by Dr. Seuss [3]. The height of each word is proportional to its trophic level. Colours indicate syntactic function; from lowest to highest mean trophic level: nouns (blue), prepositions and conjunctions (cyan), determiners (pink), adverbs (yellow), pronouns (green), verbs (red), and adjectives (purple). When a word has more than one function, the one most common in the text is used. Credit: Johnson S, Jones NS (2017) Looplessness in networks is linked to trophic coherence. Proc Natl Acad Sci USA 114(22):5618-5623. Network of concatenated words](https://scx1.b-cdn.net/csz/news/800a/2017/networkofcon.jpg)
This point's impact, Johnson continues, is based on the fact that feedforward loops can often be related to some form of feedforward control (as used, he notes, by engineers working on assisted automobile steering). "Therefore, feedforward loops in certain biological networks – gene regulatory networks, in particular, but also others such as neural networks – are thought to play an important role in how such systems work. In food webs, feedforward loops are associated with omnivorous species, which have often been reported to have an effect on ecosystem stability – although some say that effect is positive and others negative!"
The researchers are also investigating whether negentropy – the opposite of entropy, and in which a physical, thermodynamic or biological process creates order – are affected by trophic coherence. "The modern concept of entropy," Johnson points out, "comes from statistical physics and is a property of ensembles, as described above – that is, the entropy of an ensemble is simply a function of the number of elements it contains." Moreover, he adds, graph ensemble entropy has proven to be a powerful tool for understanding various network properties. We are currently studying the entropy of the coherence ensemble we defined for this work. "In general, higher trophic coherence would be associated with lower entropy states, which means that if networks are more coherent than the random expectation there must indeed be some kind of negentropic process at work." Johnson notes that the impact in this case relative to trophic coherence would be found in quantifying the extent to which different empirical networks have been driven from their maximum entropy state. "This might be the best way of discovering when there are coherence-inducing mechanisms at work, how much energy must be involved, and ultimately identifying the nature of such processes."
Phys.org also asked Johnson if there are scale boundaries to trophic coherence – for example, is trophic coherence applicable to nanoscale systems or structures, or to quantum mechanics (in which eigenvalues are highly relevant)? "This is an interesting question," he replied. "We haven't thought much about this yet – but there's no reason in principle why trophic coherence shouldn't be relevant in other settings than the ones we've considered, and at other scales. Although we've been thinking about trophic coherence as a property of networks, it could just as easily be regarded as a property of matrices, which have many different interpretations and applications in science. Could the concept of trophic coherence be extended to the complex, Hermitian matrices describing quantum operators, for instance?" (A Hermitian matrix is a square self-adjoint matrix equivalent to its own conjugate transpose.) "If so, what would the effect of coherence on eigenspectra mean for physical observables? We hope these and other open questions will attract the attention of researchers in the relevant fields, who may be able to take the work further."
Johnson also noted that while certain natural systems are unsurprising given their trophic coherence, this is not always the case. "Most of the things we measured in our set of empirical networks were actually close to what we would predict given their trophic coherence. The exceptions were a couple of food webs which, curiously, have no cycles despite being in the loopful regime – but this doesn't imply, by any means, that everything is determined by a network's trophic coherence, since there are a great many other quantities which we haven't yet considered. What was somewhat surprising, however, was that while the gene regulatory networks seem highly coherent, they are all actually rather close to what would be their random expectation, which is due to their tendency to have many basal nodes." Johnson explains that these networks – which he says underlie all the processes that cells are capable of performing, and determine the various kinds of cells they can turn into – must have been fine-tuned by evolution in myriad ways. "It seems therefore surprising that their trophic coherence shows little deviation from our random expectation. On the other hand, the metabolic networks are all highly incoherent, as compared with the random expectation, but we have as yet no idea why this might be."
Other coherence- or incoherence-inducing mechanisms would presumably alter a network in such a way that the probability of an edge occurring between two nodes depends on their trophic levels, he continues, pointing out that this might happen because trophic levels reflect some other node characteristic, their intranetwork function, or their position in one or more dimensions. "For example, in the case of food webs," he illustrates, "there are several biological features of species which are related to trophic levels, so it is natural that if a given predator has specialized in consuming species A, it is more likely to prey also on B if A and B are at similar levels. However, in some ecosystems species can also occupy different positions in space – for instance, they might exist at different depths in a lake – which could also affect coherence. Moreover, in a social network, people might interact with others according to their job, or their status – but neurons, genes, or words in a text are connected to others, which have particular functional roles. While we'd expect to find mechanisms which led to edges forming preferentially between nodes according to these kinds of features, functions, or dimensions, there are probably other ways which we haven't yet thought of."
Another question is how concepts such as trophic coherence might be understood when a distinction between excitatory and inhibitory interactions is made. "There are at least two ways in which it might be useful to define trophic levels, and thus coherence, in this case. One would be simply to attribute a negative value to inhibitory interactions, but keep other definitions broadly the same, so that trophic levels could be either positive or negative," Johnson tells Phys.org. "Another is to separate the effects of excitatory and inhibitory interactions as if they were in different networks, so that each node would have two different trophic levels, and there would be an excitatory coherence and an inhibitory one. This fits in with work currently being done on so-called multiplex networks. In the end, we would have to see which definition proves most useful for understanding real-world networks."
Moving forward, Johnson says, he and his colleagues are investigating avenues that follow from the research under discussion, such as extending the concepts of trophic levels and coherence to a broader class of networks – for example, those with weighted edges or many layers. "We then hope to use these in conjunction with other well-established network measures to identify functional groups of nodes in specific systems, such as gene regulatory networks or ecosystems. Another of our interests is the integration of these results within a more general mathematical framework relating structure and dynamics in complex systems. Finally," he concludes, "there are questions in ecology that this work might illuminate, including how best to model food webs, and whether there are network properties of ecosystems that could alert us to the risk of a tipping point, such as a cascade of extinctions."
Johnson adds that he and Jones are both working on several other topics as well as networks. "For instance, I have various ongoing collaborations with people at Warwick and Granada looking into the relationship between human conflict and geography, or how certain findings in neuroscience can be understood and modelled mathematically."
Regarding other areas of research that might benefit from their study, Johnson says that the most immediate would be complex networks and graph theory, where our results should be of interest to people studying graph ensembles, the relationships between different topological quantities, or the stability of complex, dynamical systems. "As mentioned above, there are some results which are particularly relevant for ecologists, especially those engaged in modelling ecosystems. We hope that some of these ideas will be picked up by researchers in other areas where systems can be fruitfully regarded as networks – I have mentioned genetics, but there are several others, such as neuroscience, sociology, or economics – and developed further."
More information: Looplessness in networks is linked to trophic coherence, PNAS (2017) 114(22):5618-5623, doi:10.1073/pnas.1613786114
Related:
1Trophic coherence determines food-web stability, PNAS (2014) 111(50):17923-17928, doi:10.1073/pnas.1409077111
Journal information: Proceedings of the National Academy of Sciences
© 2017 Phys.org