Modelling rare events in complex systems

NUS mathematicians have developed efficient methods to study complex energy landscapes and thermally activated events. Many problems arising from applied sciences can be abstractly formulated as a system navigating over a complex energy landscape. Well-known examples include conformational changes of bio-molecules, chemical reactions, nucleation events during phase transitions, etc. The dynamics proceed by long waiting periods around metastable states followed by sudden jumps or transitions from one state to another.
These transition events happen infrequently due to the presence of energy barriers between the metastable states, hence they are called rare events. When the rare events happen, they usually happen rather quickly and have important consequences. Typically a small amount of noise is present in the system and it is this that drives these rare events.
The objective in the study of rare events is not to keep track of the detailed dynamics of the system but rather to statistically capture the sequence of transitions between different metastable states. Therefore, the main objects which need to be computed are the transition pathways and the transition rates. The computation of these quantities represents one of the major challenges in computational science. The difficulty is mainly due to the disparity of time scales involved in the dynamics, which makes conventional simulation methods prohibitively expensive. Indeed, it takes a huge number of time steps on average to observe a transition event in these simulations.

In the last few years, Prof Weiqing REN, from the Department of Mathematics, NUS and his co-workers developed an efficient numerical method, called the string method, for the study of complex energy landscapes and noise-induced rare events. The idea is to evolve a string, which is a curve parameterised by its arc-length, in the path space by steepest descent-like dynamics. After the dynamics reach the steady state, the string converges to the minimum energy path, i.e. the transition path of maximum likelihood, and locates the transition state and the energy barriers.
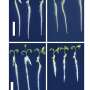
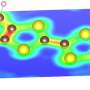
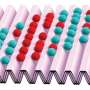
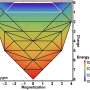
The string method has been successfully applied to many systems in different disciplines, e.g. the switching of micro magnetics, conformational changes of bio-molecules, dislocation dynamics in crystalline solids, the wetting transition on solid surface patterned with microstructures, etc. Recently, the method was employed to study the isotropic-nematic phase transition in liquid crystals. In the isotropic phase, particles in the liquid crystal are randomly packed. In contrast, the particles are well-ordered in the nematic phase (Figure 1). The isotropic-nematic phase transition is a rare event because it involves the crossing of energy barriers. In this work, Prof Ren and his student studied the isotropic-nematic phase transition in a coarse-grained space formed by two collective variables. They computed the minimum free energy path using the string method and studied the structure of the transition state. Their results revealed the multilayer structure of the critical nucleus (Figure 2). The nucleus grows further and evolves to the nematic phase after it crosses the energy barrier.
In future, the researchers intend to study the problem with additional collective variables included in the coarse-grained space. "This will help to better quantify the structure of the transition state at the microscopic level," Prof Ren said.
More information: Li Y; Ren W, "Numerical study of the isotropic-nematic phase transition in liquid crystals using the string method" Communications in Computational Physics, accepted.
Weinan E et al. Simplified and improved string method for computing the minimum energy paths in barrier-crossing events, The Journal of Chemical Physics (2007). DOI: 10.1063/1.2720838
Weinan E et al. String method for the study of rare events, Physical Review B (2002). DOI: 10.1103/PhysRevB.66.052301
Journal information: Journal of Chemical Physics , Physical Review B
Provided by National University of Singapore