Ultra-high-contrast digital sensing
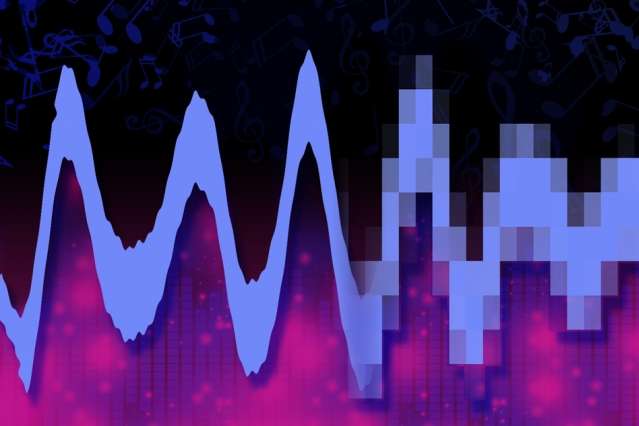
Virtually any modern information-capture device—such as a camera, audio recorder, or telephone—has an analog-to-digital converter in it, a circuit that converts the fluctuating voltages of analog signals into strings of ones and zeroes.
Almost all commercial analog-to-digital converters (ADCs), however, have voltage limits. If an incoming signal exceeds that limit, the ADC either cuts it off or flatlines at the maximum voltage. This phenomenon is familiar as the pops and skips of a "clipped" audio signal or as "saturation" in digital images—when, for instance, a sky that looks blue to the naked eye shows up on-camera as a sheet of white.
Last week, at the International Conference on Sampling Theory and Applications, researchers from MIT and the Technical University of Munich presented a technique that they call unlimited sampling, which can accurately digitize signals whose voltage peaks are far beyond an ADC's voltage limit.
The consequence could be cameras that capture all the gradations of color visible to the human eye, audio that doesn't skip, and medical and environmental sensors that can handle both long periods of low activity and the sudden signal spikes that are often the events of interest.
The paper's chief result, however, is theoretical: The researchers establish a lower bound on the rate at which an analog signal with wide voltage fluctuations should be measured, or "sampled," in order to ensure that it can be accurately digitized. Their work thus extends one of the several seminal results from longtime MIT Professor Claude Shannon's groundbreaking 1948 paper "A Mathematical Theory of Communication," the so-called Nyquist-Shannon sampling theorem.
Ayush Bhandari, a graduate student in media arts and sciences at MIT, is the first author on the paper, and he's joined by his thesis advisor, Ramesh Raskar, an associate professor of media arts and sciences, and Felix Krahmer, an assistant professor of mathematics at the Technical University of Munich.
Wraparound
The researchers' work was inspired by a new type of experimental ADC that captures not the voltage of a signal but its "modulo." In the case of the new ADCs, the modulo is the remainder produced when the voltage of an analog signal is divided by the ADC's maximum voltage.
"The idea is very simple," Bhandari says. "If you have a number that is too big to store in your computer memory, you can take the modulo of the number. The act of taking the modulo is just to store the remainder."
"The modulo architecture is also called the self-reset ADC," Bhandari explains. "By self-reset, what it means is that when the voltage crosses some threshold, it resets, which is actually implementing a modulo. The self-reset ADC sensor was proposed in electronic architecture a couple years back, and ADCs that have this capability have been prototyped."
One of those prototypes was designed to capture information about the firing of neurons in the mouse brain. The baseline voltage across a neuron is relatively low, and the sudden voltage spikes when the neuron fires are much higher. It's difficult to build a sensor that is sensitive enough to detect the baseline voltage but won't saturate during spikes.
When a signal exceeds the voltage limit of a self-reset ADC, it's cut off, and it starts over again at the circuit's minimum voltage. Similarly, if the signal drops below the circuit's minimum voltage, it's reset to the maximum voltage. If the signal's peak voltage is several times the voltage limit, the signal can thus wrap around on itself again and again.
This poses a problem for digitization. Digitization is the process of sampling an analog signal—essentially, making many discrete measurements of its voltage. The Nyquist-Shannon theorem establishes the number of measurements required to ensure that the signal can be accurately reconstructed.
But existing sampling algorithms assume that the signal varies continuously up and down. If, in fact, the signal from a self-reset ADC is sampled right before it exceeds the maximum, and again right after the circuit resets, it looks to the standard sampling algorithm like a signal whose voltage decreases between the two measurements, rather than one whose voltage increases.
Big mistakes
Bhandari and his colleagues were interested in the theoretical question of how many samples are required to resolve that ambiguity, and the practical question of how to reconstruct the original signal. They found that the number of samples dictated by the Nyquist-Shannon theorem, multiplied by pi and by Euler's number e, or roughly 8.5, would guarantee faithful reconstruction.
The researchers' reconstruction algorithm relies on some clever mathematics. In a self-reset ADC, the voltage sampled after a reset is the modulo of the true voltage. Recovering the true voltage is thus a matter of adding some multiple of the ADC's maximum voltage—call it M—to the sampled value. What that multiple should be, however—M, 2M, 5M, 10M—is unknown.
The most basic principle in calculus is that of the derivative, which provides a formula for calculating the slope of a curve at any given point. In computer science, however, derivatives are often approximated arithmetically. Suppose, for instance, that you have a series of samples from an analog signal. Take the difference between samples 1 and 2, and store it. Then take the difference between samples 2 and 3, and store that, then 3 and 4, and so on. The end result will be a string of values that approximate the derivative of the sampled signal.
The derivative of the true signal to a self-reset ADC is thus equal to the derivative of its modulo plus the derivative of a bunch of multiples of the threshold voltage—the Ms, 2Ms, 5Ms, and so on. But the derivative of the M-multiples is itself always a string of M-multiples, because taking the difference between two consecutive M-multiples will always yield another M-multiple.
Now, if you take the modulo of both derivatives, all the M-multiples disappear, since they leave no remainder when divided by M. The modulo of the derivative of the true signal is thus equivalent to the modulo of the derivative of the modulo signal.
Inverting the derivative is also one of the most basic operations in calculus, but deducing the original signal does require adding in an M-multiple whose value has to be inferred. Fortunately, using the wrong M-multiple will yield signal voltages that are wildly implausible. The researchers' proof of their theoretical result involved an argument about the number of samples necessary to guarantee that the correct M-multiple can be inferred.
"If you have the wrong constant, then the constant has to be wrong by a multiple of M," Krahmer says. "So if you invert the derivative, that adds up very quickly. One sample will be correct, the next sample will be wrong by M, the next sample will be wrong by 2M, and so on. We need to set the number of samples to make sure that if we have the wrong answer in the previous step, our reconstruction would grow so large that we know it can't be correct."
"Unlimited sampling is an intriguing concept that addresses the important and real issue of saturation in analog-to-digital converters," says Richard Baraniuk, a professor of electrical and computer engineering at Rice University and one of the co-inventors of the single-pixel camera. "It is promising that the computations required to recover the signal from modulo measurements are practical with today's hardware. Hopefully this concept will spur the development of the kind of sampling hardware needed to make unlimited sampling a reality."
More information: On Unlimited Sampling: www.dropbox.com/s/e7v4m4uhx8255tr/Unlimited%20Sampling.pdf?dl=0
Provided by Massachusetts Institute of Technology