Researchers develop mathematical method for defining electoral districts
For democratic elections to be fair, voting districts must have similar sizes. When populations shift, districts need to be redistributed - a complex and, in many countries, controversial task when political parties attempt to influence redistricting. Mathematicians at the Technical University of Munich (TUM) have now developed a method that allows the efficient calculation of optimally sized voting districts.
When constituents cast their vote for a candidate, they assume it carries the same weight as that of the others. Voting districts should thus be sized equally according to population. When populations change, boundaries need to be redrawn.
For example, 34 political districts were redrawn for the upcoming parliamentary election in Germany—a complex task. In other countries, this process often results in major controversy. Political parties often engage in gerrymandering, to create districts with a disproportionately large number of own constituents. In the United States, for example, state governments frequently exert questionable influence when redrawing the boundaries of congressional districts.
"An effective and neutral method for political district zoning, which sounds like an administrative problem, is actually of great significance from the perspective of democratic theory," emphasizes Stefan Wurster, Professor of Policy Analysis at the Bavarian School of Public Policy at TUM. "The acceptance of democratic elections is in danger whenever parties or individuals gain an advantage out of the gate. The problem becomes particularly relevant when the allocation of parliamentary seats is determined by the number of direct mandates won. This is the case in majority election systems like in USA, Great Britain and France."
Test case: German parliamentary election
Prof. Peter Gritzmann, head of the Chair of Applied Geometry and Discrete Mathematics at TUM, in collaboration with his staff member Fabian Klemm and his colleague Andreas Brieden, professor of statistics at the University of the German Federal Armed Forces, has developed a methodology that allows the optimal distribution of electoral district boundaries to be calculated in an efficient and, of course, politically neutral manner.
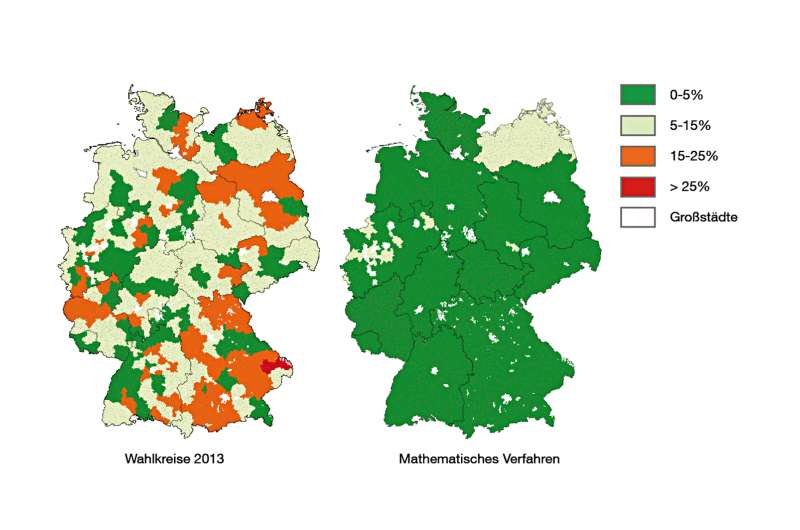
The mathematicians tested their methodology using electoral districts of the German parliament. According to the German Federal Electoral Act, the number of constituents in a district should not deviate more than 15 percent from the average. In cases where the deviation exceeds 25 percent, electoral district borders must be redrawn. In this case, the relevant election commission must adhere to various provisions: For example, districts must be contiguous and not cross state, county or municipal boundaries. The electoral districts are subdivided into precincts with one polling station each.
Better than required by law
"There are more ways to consolidate communities to electoral districts than there are atoms in the known universe," says Peter Gritzmann. "But, using our model, we can still find efficient solutions in which all districts have roughly equal numbers of constituents - and that in a 'minimally invasive' manner that requires no voter to switch precincts."
Deviations of 0.3 to 8.7 percent from the average size of electoral districts cannot be avoided based solely on the different number of voters in individual states. But the new methodology achieves this optimum. "Our process comes close to the theoretical limit in every state, and we end up far below the 15 percent deviation allowed by law," says Gritzmann.
Deployment possible in many countries
The researchers used a mathematical model developed in the working group to calculate the electoral districts: "Geometric clustering" groups the communities to clusters, the optimized electoral districts. The target definition for calculations can be arbitrarily modified, making the methodology applicable to many countries with different election laws.
The methodology is also applicable to other types of problems: for example, in voluntary lease and utilization exchanges in agriculture, to determine adequate tariff groups for insurers or to model hybrid materials. "However, drawing electoral district boundaries is a very special application, because here mathematics can help strengthen democracies," sums up Gritzmann.
More information: Andreas Brieden et al, Constrained clustering via diagrams: A unified theory and its application to electoral district design, European Journal of Operational Research (2017). DOI: 10.1016/j.ejor.2017.04.018
Provided by Technical University Munich