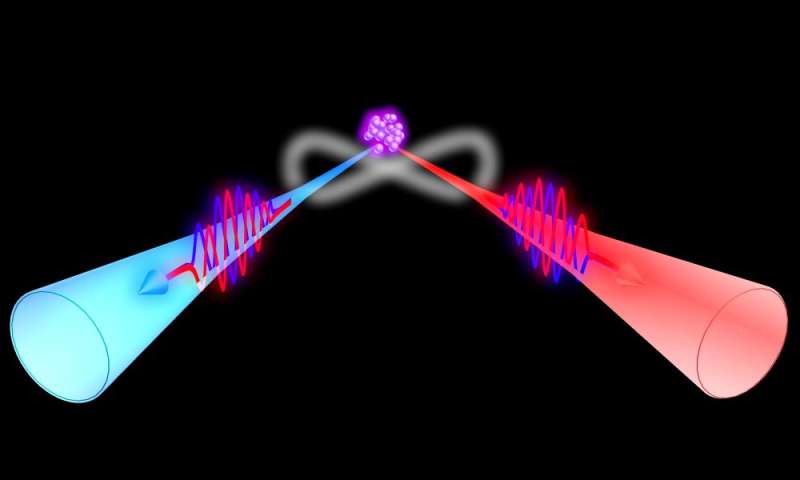
Researchers demonstrated violation of Bell's inequality on frequency-bin entangled photon pairs
Quantum entanglement, one of the most intriguing features of multi-particle quantum systems, has become a fundamental building block in both quantum information processing and quantum computation. If two particles are entangled, no matter how far away they are separated, quantum mechanics predicts that measurement of one particle leads to instantaneous wave-function collapse of the other particle.
Such "spooky action at a distance" is non-intuitive, and in 1935, Einstein attempted to use entanglement to criticize quantum mechanics to suggest that the quantum description of physical reality is incomplete. Einstein believed that no information could travel faster than light, and suggested that there might be some local hidden variable theories that could explain the world in a deterministic way, if and only if they obey realism and locality. In 1964, J. S. Bell showed that the debate can be experimentally resolved by testing an inequality; by measuring correlations between entangled parties, the result calculated from local hidden variable theories should be constrained by the Bell inequality, which, on the other hand, can be violated in the predictions of quantum mechanics.
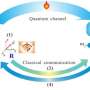
By reducing the velocity of light dramatically, researchers at the Hong Kong University of Science and Technology implemented a Bell Test and were able to generate frequency-bin entangled narrowband biphotons from spontaneous four-wave mixing (SFWM) in cold atoms with a double-path configuration, where the phase difference between the two spatial paths can be controlled independently and nonlocally.
Their findings were published in the journal Optica on April 15, 2017.
"We tested the CHSH Bell inequality and registered |S|=2.52±0.48|S|=2.52±0.48, which violates the Bell inequality |S|≤2," said Shengwang Du, professor of Physics at HKUST and the leader of the research team. "We have unambiguously demonstrated the generation of frequency-bin entangled narrowband (about 1 MHz) biphotons, which can efficiently interact with stationary atomic quantum nodes in an atom-photon quantum network. Because of their narrow bandwidth, these biphotons can be stored and retrieved from a quantum memory with high efficiency."
"Our result, for the first time, tests the Bell inequality in a nonlocal temporal correlation of frequency-bin entangled narrowband biphotons with time-resolved detection," said Xianxin Guo, a co-author of the paper. "This will have applications in quantum information processing involving time-frequency entanglement."
The study revealed temporal details that agree well with theory calculations based on quantum mechanics, and implies the possibility of encoding and decoding qubit information in the time domain.
"Our narrowband frequency-bin entangled biphoton source in this work can be ideally implemented to produce pure heralded single photons in a two-color qubit state with a tunable phase, making use of entanglement, linear optics, and time-resolved detection," said Guo.
More information: Xianxin Guo et al, Testing the Bell inequality on frequency-bin entangled photon pairs using time-resolved detection, Optica (2017). DOI: 10.1364/OPTICA.4.000388
Journal information: Optica
Provided by Hong Kong University of Science and Technology