Scientists explain the way Weyl particles 'dance' on crystal surface

Researchers at MIPT have examined the behavior of Weyl particles trapped on the surface of Weyl semimetals. Their study was published in the prestigious Rapid Communications section of Physical Review B.
The Weyl particle—or the Weyl fermion, to use a more precise term—was predicted in the early 20th century by Hermann Weyl, a German physicist. Despite his early prediction and tremendous efforts directed toward the search for the illusive Weyl particle, it was only experimentally discovered in 2015. Contrary to expectations, the Weyl was not observed in a giant collider, but in tiny crystals, which came to be known as Weyl semimetals. These materials have since attracted a lot of attention, making this research area one of the hottest in modern physics.
Weyl semimetals can be considered a 3-D equivalent of graphene, the 2-D crystal with unique properties discovered by MIPT graduates Andre Geim and Konstantin Novoselov, who were awarded the Nobel Prize in physics in 2010. Electrons in graphene and Weyl semimetals behave as massless particles akin to photons. However, unlike photons, these particles have an electric charge, making them promising for applications in electronics. As it turns out, the bizarre properties of electrons in these kinds of materials can be described in terms of topological field theory. The 2016 Nobel Prize in physics was awarded to scientists that introduced topological concepts into condensed state physics.
In a theoretical study supervised by MIPT's Prof. Vladimir Volkov, Zhanna Devizorova, a Ph.D. student at MIPT, looked into surface states of Weyl fermions, i.e., how electrons behave near the surface of a Weyl semimetal crystal. The special states of electrons near the surface of a crystal, known as electronic surface states, were predicted in the 1930s by future Nobel Prize winners Igor Tamm (USSR) and William Shockley (USA), who proposed and studied the first theoretical models of these states. However, it was not until recently that surface states gained the attention of researchers. The practical significance of this field of research is evidenced by the fact that modern microelectronics using silicon are universally based on near-surface conducting channels. However, silicon itself is not a topological material.
The behavior of any particle under an external field is determined by the dispersion law that relates the particle's energy to its momentum. According to the dispersion law, the energy spectrum of electrons in a crystal defines such electronic properties as conductivity. The bulk energy spectrum of electrons in a Weyl semimetal is described by a set consisting of an even number of Weyl cones, or valleys, centered at special points in the momentum space.
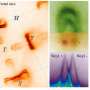
The surface of such a crystal has remarkable properties. Weyl semimetals are distinguished by the trademark energy spectrum of particles populating their surface states. In these exotic spectra, the curves that represent states with equal energy are non-closed and appear as arcs on two-dimensional momentum space. These so-called Fermi arcs connect points of the electron spectrum that belong to different Weyl cones. Unlike Weyl fermions, ordinary electrons are characterized by closed Fermi curves in the form of a circle. Until now, all theoretical descriptions of Fermi arcs have relied on complicated and obscure computer calculations based on first principles.
The MIPT-based scientists took advantage of the fact that Weyl fermions located away from the surface of the crystal obey Weyl's differential equations to derive the boundary conditions that successfully account for intervalley interactions on semimetal surface. They solved the system of Weyl's equations for two valleys "by hand," taking into account the derived boundary conditions, thus analytically finding the shape of Fermi arcs. In effect, they offered a quantitative as well as qualitative description of experimental data, and proved that Fermi arc formation is mainly driven by strong intervalley interaction under Weyl fermion scattering on crystal surface.
It is conceivable that Weyl semimetals could enable ultrafast electronics. Theoretical researchers are currently looking into principles that lay the foundation for next-generation electronic devices based on Weyl semimetals. This analytical approach is a relatively easy way of accounting for the influence of electric and magnetic fields on Weyl fermions. The heuristic potential of this approach could greatly facilitate progress toward faster and more efficient electronics.
More information: Zh. A. Devizorova et al, Fermi arcs formation in Weyl semimetals: The key role of intervalley interaction, Physical Review B (2017). DOI: 10.1103/PhysRevB.95.081302
Journal information: Physical Review B
Provided by Moscow Institute of Physics and Technology