February 21, 2017 feature
Proposed test would offer strongest evidence yet that the quantum state is real
(Phys.org)—Physicists are getting a little bit closer to answering one of the oldest and most basic questions of quantum theory: does the quantum state represent reality or just our knowledge of reality?
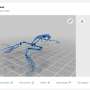
George C. Knee, a theoretical physicist at the University of Oxford and the University of Warwick, has created an algorithm for designing optimal experiments that could provide the strongest evidence yet that the quantum state is an ontic state (a state of reality) and not an epistemic state (a state of knowledge). Knee has published a paper on the new strategy in a recent issue of the New Journal of Physics.
While physicists have debated about the nature of the quantum state since the early days of quantum theory (with, most famously, Bohr being in favor of the ontic interpretation and Einstein arguing for the epistemic one), most modern evidence has supported the view that the quantum state does indeed represent reality.
Philosophically, this interpretation can be hard to swallow, as it means that the many counterintuitive features of quantum theory are properties of reality, and not due to limitations of theory. One of the most notable of these features is superposition. Before a quantum object is measured, quantum theory says that the object simultaneously exists in more than one state, each with a particular probability. If these states are ontic, it means that a particle really does occupy two states at once, not merely that it appears that way due to our limited ability to prepare particles, as in the epistemic view.
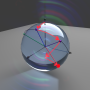
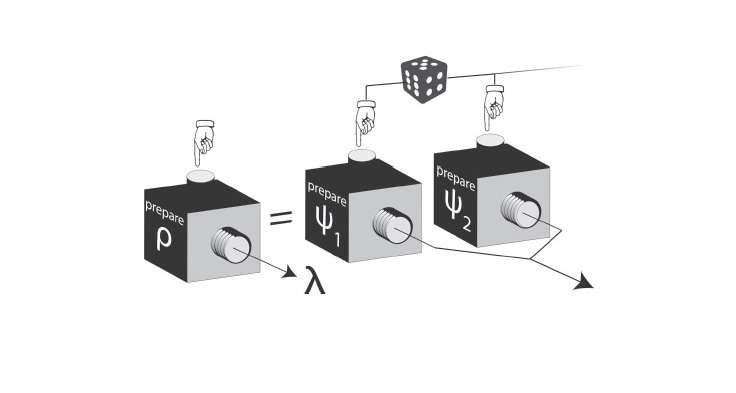
What is exactly meant by a limited ability to prepare particles? To understand this, Knee explains that different quantum states must be thought of as distributions over the possible true states of reality. If there is some overlap between these distributions, then the states of reality in which a particle can be prepared is limited.
Currently it's not clear if there actually is any overlap between quantum state distributions. If there is zero overlap, then the particle must really be occupying two states at once, which is the ontic view. On the other hand, if there is some overlap, then it's possible that the particle exists in a state in the overlapping area, and we just can't tell the difference between the two possibilities due to the overlap. This is the epistemic view, and it removes some of the oddness of superposition by explaining that the indistinguishability of two states is a result of overlap (and human limitation) rather than of reality.
Framing the question in terms of overlap offers a way to test the two perspectives. If physicists can show that the indistinguishability of quantum states can somehow be explained by reality and not overlap, then that places tighter restrictions on the epistemic view and makes the ontic view more plausible.
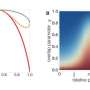
A key to such tests is that the task of discriminating between two states always has a small error involved. Having complete, omniscient knowledge about reality should improve state discrimination. But by how much? This is the big question, and physicists are trying to show that the value of this "improvement due to the increased reality of the quantum states" is very large. This would mean that the overlap plays very little, if any, role in explaining why states are indistinguishable. It's not simply that physicists cannot accurately prepare the true state of reality, it's that the indistinguishability must be thought of as a fundamental property of the quantum states themselves.
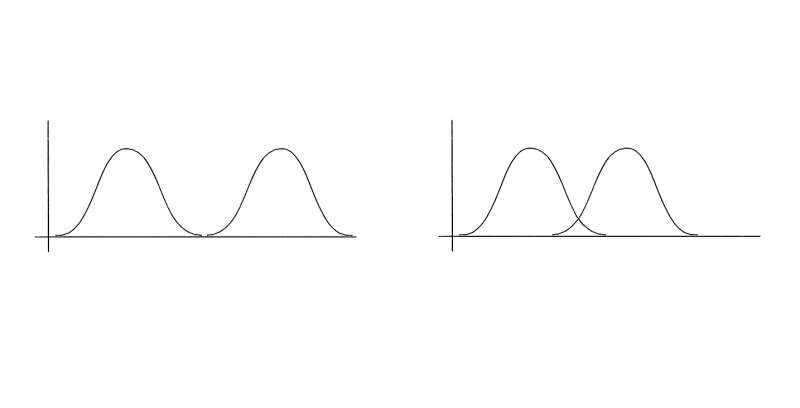
Currently, the best experimental data shows that the amount of error improvement that can be attributed to overlap is about 69%. In the new paper, Knee has proposed a way to reduce this value to less than 50% with current technology. As he explains, this would mean that "overlap is doing less than half of the necessary work in explaining the indistinguishability of non-orthogonal quantum states."
"The greatest significance of the work is the new knowledge about how to conduct experiments that can show the reality of the quantum state," Knee told Phys.org. "The big bonuses are that experimentalists will now be able to do more with less: that is, make tighter and tighter restrictions on the possible interpretations of quantum mechanics with fewer experimental resources. These experiments typically require heroic efforts, but the theoretical progress should mean that they are now possible with cheaper equipment and in less time."
To achieve such an improvement, Knee's work addresses one of the biggest challenges in this type of test, which is to identify the types of states and measurements that optimize the error improvement. This is a very high-dimensional optimization problem—with at least 72 variables, it is extremely difficult to solve using conventional optimization methods.
Knee showed that a much better approach to this type of optimization problem is to convert it into a problem that can be studied with convex programming methods. To search for the best combinations of variables, he applied techniques from convex optimization theory, alternately optimizing one variable and then the other until the optimal values of both converge. This strategy ensures that the results are "partially optimal," meaning that no change in just one of the variables could provide a better solution. And no matter how optimal a result is, Knee explains that it may never be possible to rule out the epistemic view entirely.
"There will always be wriggle room!" he said. "Certainly with the techniques known to us at the present time, a small amount of epistemic overlap can always be maintained, because experiments must be finished in a finite amount of time, and always suffer from a little bit of noise. That is to say nothing of the more wacky loopholes that a staunch epistemicist could try and jump through: for example, one can usually appeal to retrocausality or unfair sampling to get around the results of any 'experimental metaphysics.' Nevertheless, I believe that showing the quantum state must be at least 50% real is an achievable goal that most reasonable people would not be able to wriggle out of accepting."
One especially surprising and encouraging result of the new approach is that it shows that mixed states could work better for supporting the ontic view than pure states could. Typically, mixed states are considered more epistemic and lower-performing than pure states in many quantum information processing applications. Knee's work shows that one of the advantages of the mixed states is that they are extremely robust to noise, which suggests that experiments do not need nearly as high a precision as previously thought to demonstrate the reality of the quantum state.
"I very much hope that experimentalists will be able to use the recipes that I have found in the near future," Knee said. "It is likely that the general technique that I developed would benefit from some tweaking to tailor it to a particular experimental setup (for example, ions in traps, photons or superconducting systems). There is also scope for further theoretical improvements to the technique, such as combining it with other known theoretical approaches and introducing extra constraints to learn something of the general structure of the epistemic interpretation. The holy grail from a theoretical point of view would be to find the best possible experimental recipes and prove that they are as much! That is something I will continue to work on."
More information: George C. Knee. "Towards optimal experimental tests on the reality of the quantum state." New Journal of Physics. DOI: 10.1088/1367-2630/aa54ab
Journal information: New Journal of Physics
© 2017 Phys.org