Modeling the rhythmic electrical activities of the brain
Researchers studying the brain have long been interested in its neural oscillations, the rhythmic electrical activity that plays an important role in the transmission of information within the brain's neural circuits. In rats, oscillations in the hippocampus region of the brain have been shown to encode information that describes the animal's position in a physical space. In humans, neural oscillations are often studied in relation to epilepsy and various sleeping disorders though questions remain about their precise function.
For computational neuroscientists, who study how different structures in the brain process information, one interesting facet of this activity is the capacity of neural tissue to respond to external stimuli with different types of oscillations.
"These diverse responses underlie several important questions in neuroscience," explained Leandro Alonso, a computational neuroscientist and former postdoctoral fellow at Rockefeller University in New York City. "How does the same neural tissue do different things at different times? How is information altered by the connections and intrinsic dynamics of the neural circuit?"
Working with the Wilson-Cowan model, a widely-used model in computational neuroscience that describes the average activity of populations of interconnected neurons, Alonso has designed a new mathematical tool to help other neuroscientists explore the broad spectrum of responses possible from a simple neural circuit.
Alonso explains his findings this week in the journal Chaos.
"It's useful in modeling concepts in neuroscience to have a system that will yield a diverse range of behaviors for small changes of a control parameter, as this may help offer some insights about how the same neural tissue displays different responses," Alonso said, whose research was funded by a fellowship from the Leon Levy Foundation.
Alonso's model builds its foundation on a mathematical concept called a "nonlinear oscillator." When oscillators, quantities that are in a state of repetitive fluctuation, are linear, the oscillator responds to an external input by mirroring its rhythm or frequency. In contrast, with nonlinear oscillators, the frequency of the oscillatory response varies from the frequency of the input. Differences can often be observed as well in the shape of the oscillations of the response.
Although nonlinear oscillation is not specific to neuroscience, Alonso was pleasantly surprised at how well it integrated with the Wilson-Cowan model to offer some insight on how neurons can be connected so that they yield a diverse range of oscillations when stimulated.
"When you observe the complexity of oscillatory phenomena in the brain, it seems reasonable to assume that it can be explained by an equally complex system that underlies these oscillations," Alonso said. "Whether this is the case or not, it is interesting that a simple circuit with just two populations of interconnected neurons can produce a similarly diverse repertoire of activity."
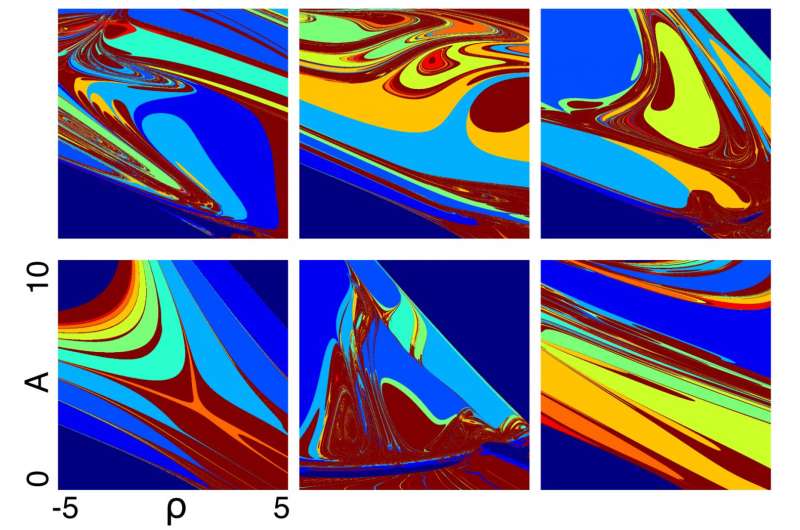
In his article, Alonso includes a series of colorful "locking diagrams" that visually represent the variety of responses that are possible as the parameters of the external stimulus, such as its frequency and amplitude, are subtly changed.
"The different colors show how the frequency of the response has changed," Alonso explained.
Alonso, who first began studying the nonlinear oscillations of neurons while training at the Dynamical Systems Laboratory at the University of Buenos Aires, believes that his model can aid other computational neuroscientists working on their own models.
"I hope the procedure will be helpful for deriving the parameters of neural circuits such as their connectivities, so that an incoming oscillation will trigger several different types of responses," said Alonso. "It's also possible that the broader discussion of nonlinear oscillations could be helpful to scientists examining other biological systems that exhibit comparable dynamic responses."
Alonso's next research project will be to investigate the properties of systems that have multiple neural circuits with these properties connected together.
More information: "Nonlinear resonances and multi-stability in simple neural circuits," Chaos: An Interdisciplinary Journal of Nonlinear Science, DOI: 10.1063/1.4974028
Journal information: Chaos
Provided by American Institute of Physics