July 1, 2016 feature
'Quantum' bounds not so quantum after all
(Phys.org)—Quantum bounds are numbers (such as 4, 6, and 2√2) that naturally appear in quantum experiments, similar to how the number π emerges in circles. But just as how π pops up in a wide variety of areas beyond circles, in a new study physicists have found that quantum bounds are not exclusive to quantum theory but also emerge in purely classical experiments. The results suggest that attempts to define quantumness should not be concerned with quantum bounds, since there is nothing inherently quantum about them.
The physicists, Diego Frustaglia et al., at the University of Sevilla in Spain, have published a paper on the emergence of quantum bounds in classical experiments in a recent issue of Physical Review Letters.
Different experiments, same bounds
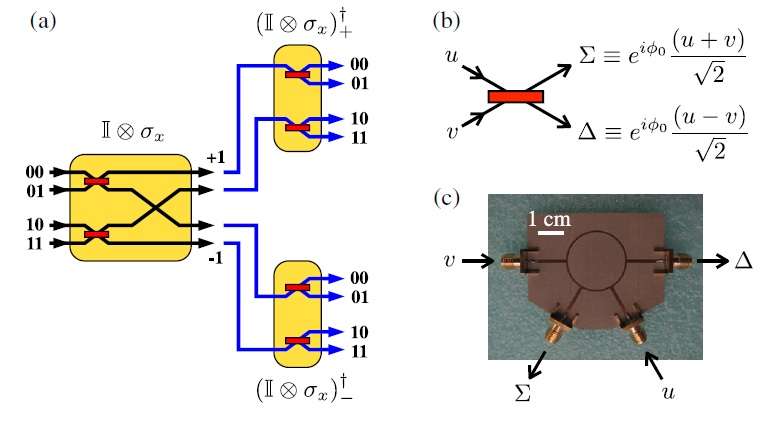
In their study, the researchers performed three classical experiments that correspond to three famous quantum experiments involving quantum bounds. These quantum experiments are a sequential version of the Bell inequality and two other related quantum inequalities, all of which are used to distinguish between quantum and classical phenomena.
In order to show that a system exhibits quantum effects, these experiments traditionally attempt to show that a system can violate a quantum inequality. The greater the violation, the more quantum the system. The maximum violation of a quantum inequality is the quantum bound. The quantum bounds arise from probability distributions in the experiments and are specific numbers—for instance, the Bell inequality has a quantum bound of 2√2 (approximately 2.82), which is known as Tsirelson's bound. The other two inequalities addressed here have quantum bounds of 4 and 6. Both theoretically and experimentally, no violation of a quantum inequality has ever surpassed these bounds.
In the new study, the researchers showed that these same quantum bounds emerge in experiments in which classical waves travel along an ordinary transmission line. The researchers found that the probabilities originating from the detection of wave intensities at the end of the transmission line follow the same distribution as the probabilities of detecting violations of the quantum inequalities. Specifically, the classical experiments yield bounds of 2.78, 3.93, and 5.93 for the three analogous experiments. In all three cases, these values are actually slightly closer to their theoretical values mentioned above than the values obtained in quantum experiments are, providing strong evidence that both quantum and classical experiments produce the same bounds.
Interpreting the results
One of the many implications of the study is that it offers new insight into what it means to be quantum. By showing that quantum bounds are not unique to quantum theory, but are universal bounds, the findings show that ongoing attempts to define quantum theory should not focus on these bounds.
Instead, the results provide a clue for finding a true quantum feature by revealing an important difference between the way in which the classical and quantum systems produce the same bounds. While the classical systems require some kind of extra resource, such as memory, the quantum systems do not. So a complete description of quantum theory should explain how quantum systems can violate the same bounds that classical systems do, but without using extra resources.
As the researchers explain, this approach of investigating classical systems to better understand quantum mechanics tends to be the opposite of most research.
"We somehow reverted the strategy followed by the founders of quantum theory," Frustaglia told Phys.org. "In the early times of quantum mechanics, microscopic systems were subject to an intense questioning naturally biased towards classical physics. The result was a set of oddities interpreted as the paradigmatic features of the quantum realm: the particle-wave duality (is it a particle or a wave?), the Schrödinger's cat (is it dead or alive?), and the Heisenberg's uncertainty principle (where and how fast is it?).
"As a consequence, it was soon understood that quantum systems should be interrogated in their own specific language, eventually provided by modern quantum theory. It is then pertinent to address the possibility of interrogating classical systems with questions inspired by quantum physics. This is what we did, indeed, finding that classical systems with an underlying wave mechanism answer these questions in the same way truly quantum systems do. But one has to choose your system carefully: one would not be able to make it by using plain balls, for instance."
In the future, the physicists plan to investigate how the universal bounds might emerge in the first place.
"Our results show that the 'quantum' bounds are common to many physical theories," said coauthor Adán Cabello at the University of Sevilla. "This suggests that the reason for these bounds is something very simple and arguably inherent to the kind of theories we are interested in: theories in which 'measurements' produce repeatable results which are not affected by some other measurements.
"Surprisingly, this simple idea singles out many 'quantum' bounds. When we adopt this perspective, what is really significant is the fact that these bounds are actually reachable in nature. This shows that no hypothetical physical principle is acting and leads us to the conjecture that one of the physical principles that singles out quantum theory is precisely that one: There is no principle determining the probabilities of the outcomes of these 'measurements.'
"One plan is to prove that this simple idea is responsible for all quantum bounds. Another plan is to test whether it is really true that these bounds can be reached with quantum systems. So far, and only very recently, H. S. Poh et al. have confirmed the so-called Tsirelson bound, 2√2, with four significant digits, but there is absolutely no experimental evidence of whether we can 'touch' these bounds in other scenarios. Also, it would be great to derive quantum theory from the assumption that there are no laws of nature determining or limiting the probabilities of measurement outcomes, and that the whole machinery of the theory follows from the aesthetic preference in the way we define 'measurements.'"
Finally, the physicists also plan to investigate potential applications, such as building quantum technologies with the help of classical systems.
"Although inefficient in the sense that they require more memory or space, classical systems are sometimes better to produce 'quantum' numbers than quantum systems themselves," Frustaglia said. "In contrast to quantum systems, which are very sensitive to the environment, the wires in our experiment can be bent, moved, heated, etc., and the results are the same. This suggests a future in which quantum technologies are actually built using quantum systems plus classical systems imitating quantum systems. It also raises the question as to whether similar 'quantum' features with potential functionalities can emerge in other supports as complex networks of artificial or biological nature. An appropriate answer to this questions requires multidisciplinary efforts that we are presently considering."
More information: Diego Frustaglia et al. "Classical Physics and the Bounds of Quantum Correlations." Physical Review Letters. DOI: 10.1103/PhysRevLett.116.250404. Also at arXiv:1511.08144 [quant-ph]
Journal information: Physical Review Letters
© 2016 Phys.org