Electromagnetic metamaterials with zero-refractive index for sub-wavelength photonics
Materials scientists can produce sub-wavelength artificial structures (split rings, honeycomb shapes and many more) to interact with electromagnetic waves so that the propagation of waves can be arbitrarily controlled to achieve desired effects. Among the myriad of these 'metamaterials', metal-dielectric periodic multilayers—hyperbolic metamaterials (HMMs)—are of particular interest. In spite of their simple structure, HMMs have the potential for unique optical applications including super-resolution lens, sub-wavelength interference and enhancing the emission of single-photon sources.
Now, Satoshi Ishii, at the International Center for Materials Nanoarchitectonics (MANA), NIMS, and Evgenii Narimanov at Purdue University, USA, analytically describe non-local optical topological transition in HMMs for the first time and unveil unique optical properties at the critical states.
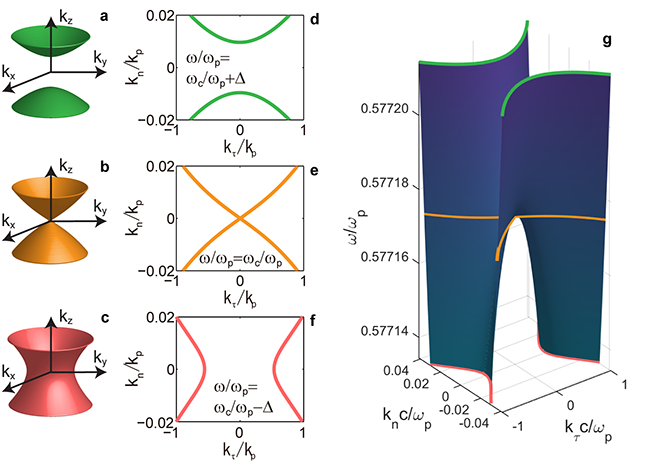
So far, most researchers have treated HMMs as effectively homogenous media based on effective medium theory. Following this theory, an HMM behaves either like a 'metal' (reflects light) or like a 'dielectric' (refracts light in the negative direction) depending on the frequency of incident light.
In this research, the scientists succeeded in analytically demonstrating the transition between these two types of states induced by the non-local topological transition (see Figure 1). Furthermore, they found that in response to incoming light at the critical state, an HMM exhibits peculiar optical properties such that its effective refractive index is zero (see Figure 2) and the refraction becomes conical.
Based on these findings, the team is going to apply HMMs for the development of novel nanophotonic elements and photonic integrated circuits by an in-depth analysis of the critical states caused by the non-local topological transitions.
More information: Satoshi Ishii et al. Non-local Optical Topological Transitions and Critical States in Electromagnetic Metamaterials, Scientific Reports (2015). DOI: 10.1038/srep17824
Journal information: Scientific Reports
Provided by National Institute for Materials Science