November 12, 2015 weblog
Computer scientist claims to have solved the graph isomorphism problem
(Phys.org)—László Babai with the Department of Computer Science and Mathematics at the University of Chicago has caused a lot of excitement in the computer science community by announcing recently during a lecture that he had developed an algorithm that solves the graph isomorphism problem. Though not as well known, it is comparable to someone solving the famous traveling salesmen problem.
The new algorithm, if it passes muster with other researchers, is not likely to cause any changes that non-computer people will notice, but solving it is an impressive achievement. Many in the field have thought doing so was impossible.
Computer science at its root is very simple—get a computer to perform a calculation we want done. Developing an algorithm that sorted records in a database, for example, was a big deal many years ago because it meant humans no longer had to do it by hand. Unfortunately, it has proven to be exceptionally difficult to get a computer to perform some other calculations, like asking it to tell a salesmen which is the best route for him, given a certain number of parameters. For a computer to do it, means grinding through all the options, which is fine for simple routes with few nodes—add hundreds, thousands or millions though, and the computer will be at it longer than the person waiting for it will live. It would be better if someone could figure out a way to tell the computer how to do it in a smarter, more efficient way—and that is what lies at the heart of computer science.
Over time, computer scientists have come up with a way to separate the easy or simple types of algorithm objectives, from those that are hard, or even thought to be impossible. Those that are relatively easy are denoted by P, because they can be run in polynomial time. Those that are hard are deemed Nondeterministic Polynomial, or just NP. The hardest of all are referred to as NP complete.
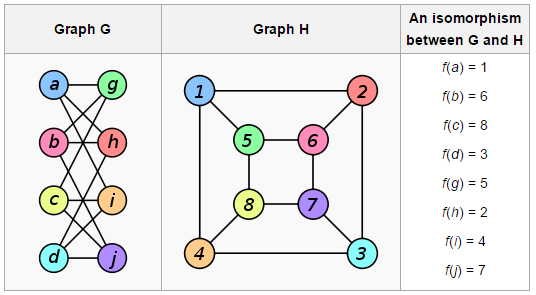
The graph isomorphism problem has been labeled as NP, though some have suggested it should be NP complete—it involves trying to create an algorithm able to look at two networks (with nodes and links between them) and report back if they are the same. Again, this is pretty simple if the network is small, but adding more complexity makes it increasing difficult to churn through. To solve this problem would require developing an algorithm that finds an answer in smart way, rather than just having a computer grind through all the options—and that is the type of algorithm that Babai believes he has created. Unfortunately, an algorithm has not yet been created to test such algorithms, thus, it will have to be vetted by other experts in the field before it can be labeled as a success.
More information: people.cs.uchicago.edu/~laci/quasipoly.html
© 2015 Phys.org