Upgrading the quantum computer
Theoretical physicists have proposed a scalable quantum computer architecture. The new model, developed by Wolfgang Lechner, Philipp Hauke and Peter Zoller, overcomes fundamental limitations of programmability in current approaches that aim at solving real-world general optimization problems by exploiting quantum mechanics.
Within the last several years, considerable progress has been made in developing a quantum computer, which holds the promise of solving problems a lot more efficiently than a classical computer. Physicists are now able to realize the basic building blocks, the quantum bits (qubits) in a laboratory, control them and use them for simple computations. For practical application, a particular class of quantum computers, the so-called adiabatic quantum computer, has recently generated a lot of interest among researchers and industry. It is designed to solve real-world optimization problems conventional computers are not able to tackle. All current approaches for adiabatic quantum computation face the same challenge: The problem is encoded in the interaction between qubits; to encode a generic problem, an all-to-all connectivity is necessary, but the locality of the physical quantum bits limits the available interactions.
"The programming language of these systems is the individual interaction between each physical qubit. The possible input is determined by the hardware. This means that all these approaches face a fundamental challenge when trying to build a fully programmable quantum computer," explains Wolfgang Lechner from the Institute for Quantum Optics and Quantum Information (IQOQI) at the Austrian Academy of Sciences in Innsbruck.
Fully programmable quantum computer
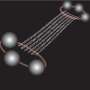
Theoretical physicists Wolfang Lechner, Philipp Hauke and Peter Zoller have now proposed a completely new approach. The trio, working at the University of Innsbruck and the IQOQI, suggest overcoming the challenges by detaching the logical qubit from the physical implementation. Each physical qubit corresponds to one pair of logical qubits and can be tuned by local fields. These could be electrical fields when dealing with atoms and ions or magnetic fields in superconducting qubits. "Any generic optimization problem can be fully programmed via the fields," explains co-author Philipp Hauke from the Institute for Theoretical Physics at the University of Innsbruck, Austria. "By using this approach we are not only avoiding the limitations posed by the hardware but we also make the technological implementation scalable."
Integrated fault-tolerance
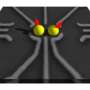
Because of the increased number of degrees of freedom, which could also lead to non-physical solutions, the physicists arrange the qubits in a way that four physical qubits interact locally.
"In this way we guarantee that only physical solutions are possible," explains Wolfgang Lechner. The solution of the problem is encoded redundantly in the qubits. "With this redundancy our model has also a high fault-tolerance," says Lechner. The new architecture can be realized on various platforms ranging from superconducting circuits to ultracold gases in optical lattices. "Our approach allows for the application of technologies that have not been suitable for adiabatic quantum optimization until now," says the physicist. Lechner, Hauke and Zoller have introduced this new model in the journal Science Advances. The scientific community has also expressed great interest in the new model.
Peter Zoller is convinced: "The step from mechanical calculators to fully programmable computers started the information technology age 80 years ago. Today we are approaching the age of quantum information."
A patent for the new quantum computer architecture has been submitted this year. The scientists are financially supported by the Austrian Science Fund (FWF) and the European Research Council (ERC) among others.
More information: A quantum annealing architecture with all-to-all connectivity from local interactions. W. Lechner, P. Hauke, P. Zoller. Sci. Adv. 1, e1500838 (2015). DOI: 10.1126/sciadv.1500838
Journal information: Science Advances
Provided by University of Innsbruck