October 21, 2015 feature
Physicists experimentally realize a quantum Hilbert hotel
(Phys.org)—In 1924, the mathematician David Hilbert described a hotel with an infinite number of rooms that are all occupied. Demonstrating the counterintuitive nature of infinity, he showed that the hotel could still accommodate additional guests. Although clearly no such brick-and-mortar hotel exists, in a new paper published in Physical Review Letters, physicists Václav Potoček, et al., have physically realized a quantum Hilbert hotel by using a beam of light.
In Hilbert's thought experiment, he explained that additional rooms could be created in a hotel that already has an infinite number of rooms because the hotel manager could simply "shift" all of the current guests to a new room according to some rule, such as moving everyone up one room (to leave the first room empty) or moving everyone up to twice their current room number (to create an infinite number of empty rooms by leaving the odd-numbered rooms empty).
In their paper, the physicists proposed two ways to model this phenomena—one theoretical and one experimental—both of which use the infinite number of quantum states of a quantum system to represent the infinite number of hotel rooms in a hotel. The theoretical proposal uses the infinite number of energy levels of a particle in a potential well, and the experimental demonstration uses the infinite number of orbital angular momentum states of light.
The scientists showed that, even though there is initially an infinite number of these states (rooms), the states' amplitudes (room numbers) can be remapped to twice their original values, producing an infinite number of additional states. On one hand, the phenomena is counterintuitive: by doubling an infinite number of things, you get infinitely many more of them. And yet, as the physicists explain, it still makes sense because the total sum of the values of an infinite number of things can actually be finite.
"As far as there being an infinite amount of 'something,' it can make physical sense if the things we can measure are still finite," coauthor Filippo Miatto, at the University of Waterloo and the University of Ottawa, told Phys.org. "For example, a coherent state of a laser mode is made with an infinite set of number states, but as the number of photons in each of the number states increases, the amplitudes decrease so at the end of the day when you sum everything up the total energy is finite. The same can hold for all of the other quantum properties, so no, it is not surprising to the trained eye."
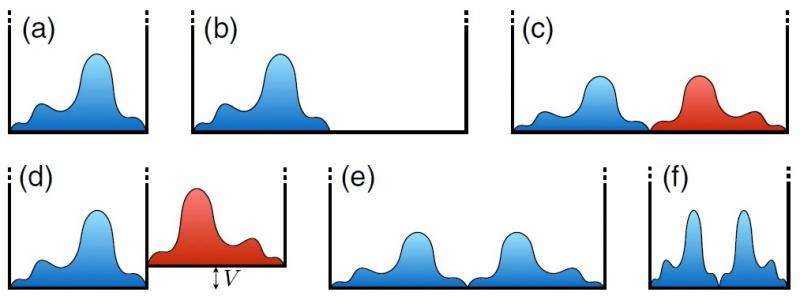
The physicists also showed that the remapping can be done not only by doubling, but also by tripling, quadrupling, etc., the states' values. In the laser experiment, these procedures produce visible "petals" of light that correspond to the number that the states were multiplied by.
The ability to remap energy states in this way could also have applications in quantum and classical information processing, where, for example, it could be used to increase the number of states produced or to increase the information capacity of a channel.
More information: Václav Potoček, et al. "Quantum Hilbert Hotel." Physical Review Letters. DOI: 10.1103/PhysRevLett.115.160505
Journal information: Physical Review Letters
© 2015 Phys.org