July 7, 2015 feature
Decoding the brain: Scientists redefine and measure single-neuron signal-to-noise ratio
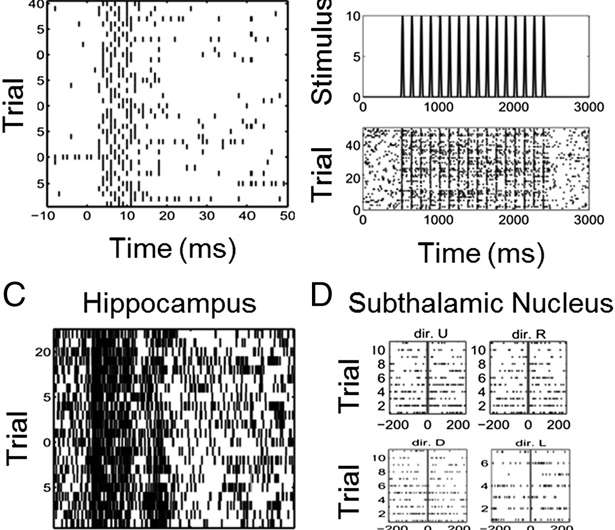
(Phys.org)—The signal-to-noise ratio, or SNR, is a well-known metric typically expressed in decibels and defined as a measure of signal strength relative to background noise – and in statistical terms as the ratio of the squared amplitude or variance of a signal relative to the variance of the noise. However, this definition – while commonly used to measure fidelity in physical systems – is not applicable to neural systems, because neural spiking activity (in which electrical pulses called action potentials travel down nerve fiber as voltage spikes, the pattern of which encodes and transmits information) is more accurately represented using point processes (random collections of points, each representing the time and/or location of an event).
Recently, scientists at the University of Liverpool and Massachusetts Institute of Technology refined the signal-to-noise ratio as an estimate of a ratio of expected prediction errors, and moreover extended the standard definition to one appropriate for single neurons using point process generalized linear models (PP-GLM) – a flexible generalization of ordinary linear regression that allows for response variables that have error distribution models other than a normal distribution. The researchers conclude that their study provides a straightforward method for determining the signal-to-noise ration of single neurons – and by generalizing the standard SNR metric, they were able to explicitly characterize the acknowledged fact that individual neurons are noisy transmitters of information. The scientists state that their new approach allows SNR computation on the same decibel scale for neurons and man-made systems, and moreover applies to any analysis in which a generalized linear model can be used as a statistical model – including clinical trials, observational studies, and the optimization and evaluation of neural prostheses.
Dr. Gabriela Czanner and Prof. Emery N. Brown discussed the paper that they and their colleagues published in Proceedings of the National Academy of Sciences. As might well be imagined, the scientists faced a number of challenges in conducting their study. "Neurons communicate through spiking activity in two ways – spike intensity modulation or spike timing patterns," Czanner tells Phys.org. "In our work, in which the fundamental challenge was to differentiate signal from noise in neuronal spiking, we focused on spike intensity. This required identifying the components that cause neurons to spike – or as Rieke and his colleagues wrote1, 'To make meaningful estimates of information transmission we need to understand something about the structure of the neural code.'"
Taking their lead from this quote, the scientists realized that in the case of single neurons, the factors that modulate the spiking activity are the stimulus, biophysical properties of the neuron, thermal noise, and activity of neighboring neurons. They then employed statistics to show that the signal regularity in the data that can be explained by stimulus and the neuron's biophysical properties, while noise comprises the remaining neural spiking dynamics not captured by the stimulus and biophysical components.
That said, Czanner points out, previous formulations of neural SNR – for example, information theory adapted to derive Gaussian upper bounds on individual neuron SNR, and coefficients-of-variation and Fano factors (two measures of dispersion of a probability distribution or frequency distribution) based on spike counts – fail to consider the point process nature of neural spiking activity. (A Gaussian distribution is a continuous probability distribution used to represent real-valued random variables whose distributions are not known.) Moreover, these measures and the Gaussian approximations are less accurate for neurons with low spike intensity modulation or when information is contained in precise spike timing patterns.
Brown notes that while the standard SNR definition assumes that a system's measurements have a Gaussian distribution and that the noise is added to the signal, neural systems produce binary observations in short time intervals – that is, a distribution summarizing the number of events in a short time interval, and when the probability of number of observations depend on the number of observations in previous time intervals. These observations are more accurately modeled as a point process, and therefore differ significantly from Gaussian distributions and from standard Binomial distributions. "Moreover," he adds, "these observations are affected by both the signal and the noise in the neural system – so the relationship is not additive."
Relatedly, he adds, it was vital to show that the neuronal signal-to-noise ratio (SNR) estimates a ratio of expected prediction errors rather than the standard SNR definition of signal amplitude squared and divided by the noise variance. "Neurons emit binary electrical discharges, called spikes, which are believed to be elementary unit of neural communication," Brown tells Phys.org. "Hence, it's important to find out precisely how much information and noise there is in the spikes."
Another challenge was determining that single neuron SNRs range from −29 to −3 decibels (dB), which meant selecting appropriate approximating models of the spiking activity. "The model has to be tailored to each neuron," Czanner stresses, "thus reflecting neurons' own specific electrophysiology and the type of the stimulation, which was either explicit or implicit. To achieve this we analyzed the SNR metric from the perspective of statistical concepts." She says that showing that traditional SNR is a random quantity that estimates a ratio of expected prediction errors allowed them to extend the SNR standard definition to one appropriate for single neurons by representing neural spiking activity using a point process generalized linear model (PP-GLM).
"We estimate prediction errors using residual deviances from PP-GLM fits," she continues. "Because the deviance is an approximate chi-squared random variable whose expected value is the number of degrees of freedom, we compute a bias-corrected SNR estimate appropriate for single neuron analysis and use the bootstrap to assess its uncertainty." In analyzing four neuroscience systems experiments, the researchers were thereby able to show that the SNRs of individual neurons have – as Brown says they expected – these very low decibel values. "In other words, by generalizing the standard SNR metric we make explicit the well-known fact that individual neurons are highly noisy information transmitters – and at the same time, our framework expresses this SNR ratio for neurons in the same units as that used for more standard Gaussian additive noise systems."
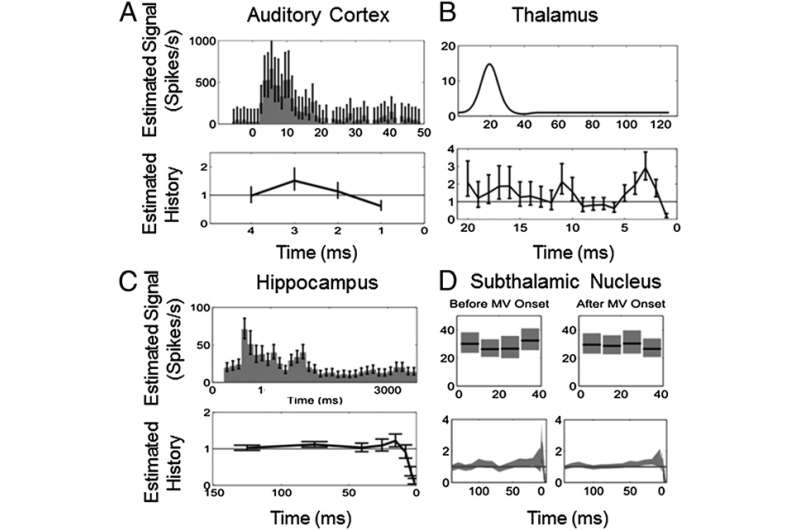
Interestingly, by calculating spiking history SNR (as is allowed by their generalized SNR definition), the scientists demonstrated that taking into account the neuron's biophysical processes – such as absolute and relative refractory periods (the periods after the action potential, when the neuron cannot spike again or can spike with low probability, respectively), bursting propensity (the period of a neuron's rapid action potentials ), local network dynamics, and, in this case, spiking history – is often a more informative predictor of spiking propensity than the signal or stimulus activating the neuron.
An important step in their investigation was to acknowledge that SNR is an estimator or a statistic, meaning that it has statistical properties that need to be evaluated. "The values of the SNR estimate are random, and so change if an experiment is repeated," Czanner says. "We therefore had to identify these properties in order to be certain that the estimate is constructed in a principled way." She notes that a key property of the SNR estimator is that it is biased, because by definition it always gives a positive value even when there is no signal. "To this end, we proposed a simple bias adjustment that worked well in simulation studies."
In reviewing their research, Czanner and Brown identified the key innovations the team developed used to address these myriad challenges:
● Determining that the quantity being estimated by the SNR is a ratio of prediction errors
● Employing the PP-GLM framework to estimate deviances as a generalization of sums of squares (is a mathematical approach to determining the dispersion of data points) so that the concept of the SNR can be extended to neurons and agrees with the concept used for Gaussian systems
● Defining a way to take account of non-signal yet relevant covariates that also affect the spiking propensity of the neuron, which we accomplished using the linear terms from the Volterra series approximation to the log of the conditional intensity function expanded in terms of the stimulus and the spiking history
● Determining that the numerator and denominator are both approximate chi-squared random variables whose means give approximations to the appropriate bias corrections, allowing the team to compute the approximate bias correction to the biased SNR estimate
● Reporting the SNR for implicit and explicit neural stimuli (those attended to or not, respectively)
● Being able to compute the SNR on the same decibel scale for neurons and man-made systems by using appropriate GLM models for each
In their paper, the researchers state that their redefined SNR is extensible to any generalized linear model in which the factors modulating the response can be expressed as separate components of a likelihood function (a function of the parameters of a statistical model). "Our SNR metric is applicable to any system whose measurements can be described via a generalized linear model," Czanner tells Phys.org. "The idea is to fit the model to the data, which effectively estimates the signal and the noise. (The model needs to be validated via, for example, standard goodness-of-fit criteria and autocorrelation tests) The new SNR can then be calculated by using deviances that generalize the concept of error sum of squares (a mathematical determination of the dispersion of data points) to generalized linear models. This means that the SNR is defined for all generalized linear models where the signal and non-signal components can be separated and hence estimated as different parts of a generalized linear model – and in fact, one of the key ideas in our work was to define the approximating model as the logarithm of conditional intensity, which allowed us to separate the signal or stimulus from the neuron's own biophysical properties."
In terms of next steps, the scientists are planning to extend the SNR definition to analyze the SNR of neuronal ensembles, in which several neurons communicate with each other. "This is a so-called multivariate case where several neurons are considered at the same time," Brown says, "and we'd like to know how ensemble SNR represents a relevant signal or stimulus."
The scientists say that the areas of research that might benefit from their new SNR concept are limitless. "Our definition applies readily to any situation in which a generalized linear model can be used as a statistical model, such as areas of research where measurements do not follow a Gaussian distribution n and/or when the noise is not additive and/or correlated," Czanner tells Phys.org. For example," she illustrates, "we are considering developing SNR metrics for evaluation of strength of surrogate biomarkers in clinical trials and observational studies, in which the surrogate biomarkers can be electrophysiological measurements from a human diabetic retina with the signal being the stage of diabetic retinopathy, or surrogate markers of retinal damage in malarial retina where the signal is the extend of brain swelling."
Brown also sees their SNR approach being used to accurately evaluate neuronal signal information. "We therefore envision that in the future this will reinforce the search for neurons that carry maximal information for the purpose of neural prostheses – and in this scenario, neural SNR may also be used to evaluate the performance of neural prostheses devices."
More information: Measuring the signal-to-noise ratio of a neuron, Proceedings of the National Academy of Sciences, (2015) 112:23 7141-7145, doi:10.1073/pnas.1505545112
Related:
1Spikes: Exploring the Neural Code, Fred Rieke and David Warland, A Bradford Book – Reprint edition (June 25, 1999), ISBN-13: 978-0262681087
Journal information: Proceedings of the National Academy of Sciences
© 2015 Phys.org