November 20, 2014 feature
Physicists study magnetism with the roles of position and momentum reversed
(Phys.org) —Normally, the strength of a magnetic field increases as you get closer to a magnet and decreases as you move further away—a concept easily understood when placing magnets near a refrigerator, for instance. But recent research has shown that exotic "momentum-space artificial magnetic fields" can be created where the strength of the magnetic field depends on how fast a particle moves, instead of where the particle is. In other words, the roles of position and momentum are swapped.
Now in a new paper, physicists have explored these ideas further, especially at the quantum level. They show how current experiments can be modified to study the motion of a quantum particle in a momentum-space magnetic field. They explain that these systems will be able to experimentally realize a "wonderland of new physics," such as magnetism on a torus, for the first time.
The physicists, Hannah M. Price, Tomoki Ozawa, and Iacopo Carusotto at the INO-CNR BEC Center and the University of Trento, Italy, have published their paper discussing momentum-space magnetism in a recent issue of Physical Review Letters.
"Magnetism is fundamental in many areas of physics, and it leads to many fascinating phenomena," Price told Phys.org. "Physicists use mathematical equations to capture the behavior of a quantum particle in a magnetic field. These equations have a particular, beautiful mathematical structure. But we can also reverse this logic. If we engineer or find an equation with this particular mathematical structure, the behavior of a particle will be like that of a particle in an 'artificial magnetic field,' even if the 'field' has a completely different underlying physical origin. As has been known for a long time, this beautiful mathematical structure can be found or created in many different physical contexts. This is a really powerful tool that physicists use to engineer and learn more about magnetism."
As the scientists explain, one of the ideas that physicists use a lot in quantum mechanics is the deep connection between the position and momentum of a particle.
"We can either view our problem in terms of all the possible 'position states' of a particle or equally in terms of all the possible 'momentum states,'" Price explained. "Depending on the viewpoint we choose, our mathematical equations will have a different form, and so we usually choose the viewpoint that gives us the easiest equations to solve and understand. The beautiful mathematical structure described above appears when we have a magnetic field and we look at our equations in terms of 'position states.'
"However, what if we could find equations in terms of 'momentum states' that had an analogous mathematical structure? Then we could draw an analogy with magnetism: we would get the same quantum physics but where the 'position' must be swapped everywhere with the 'momentum.'
"The equations could be understood as describing a particle in an 'artificial momentum-space magnetic field.'"
As has been previously shown by other physicists, it turns out that momentum-space magnetic fields are indeed real. They occur when energy bands with Berry curvature are created, and a weak additional external potential is added.
"A key message in our paper is to say, ok you have found this quantum equation with a'momentum-space magnetic field,' so why don't you solve it to look at the quantum dynamics of a particle?" Price explained. "You have all the ingredients that you need to study the quantum physics of a particle in a magnetic field (because the mathematical structure is the same), but now with position and momentum swapped. In this way, we will go from this complicated system that physicists find hard to understand (the geometrical energy bands with an additional potential) to one that we find easy to understand (magnetism)."
While scientists have previously made a similar point about the semiclassical physics, this is the first time that it has been understood in general about the quantum physics.
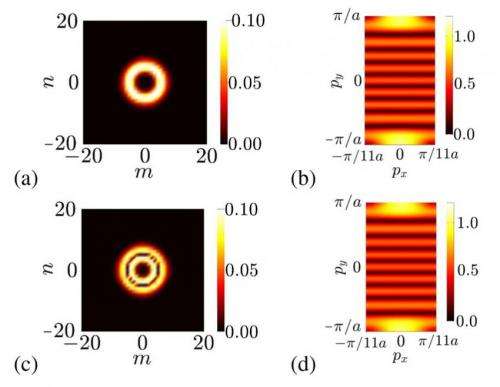
"One of our main contributions is to say that experimentalists can use this analogy to study magnetism in new ways," Price said. "Momentum space can sometimes be very different than real space, as, for some systems, momentum space is like a torus or a doughnut. Then if you increase your momentum enough, eventually you will end up in the same momentum state that you began in. So now when we study our equations, the analogy is with a particle in an artificial magnetic field in momentum space on a torus. The quantum physics of a particle in a magnetic field on a torus has never been studied experimentally before in any context (but it has been studied theoretically), and we propose exactly how it could be done in current experiments by exploiting a momentum space magnetic field."
To experimentally demonstrate these concepts, the scientists propose to use ultracold gases, as a weak harmonic trap could be added with laser beams or magnetic fields. Experimentally, it won't be easily possible to switch the momentum-space magnetic field on and off. However, by switching the harmonic trap on and off, physicists will still be able to study the system. The scientists explain that, in the analogy with magnetism, this is like changing the particle's mass, where no harmonic trap is like having an infinitely large mass. When a particle is infinitely heavy, it won't have any kinetic energy in momentum space, meaning it won't be able to move in momentum space. Since magnetic fields affect a particle as it moves, if it has an "infinite mass" in this analogy, the particle won't feel the momentum-space magnetic field.
"Our work is about exploring old answers to new questions, to the benefit of both the old and new research field," Price said. "Scientists know a lot about magnetism and have been studying the quantum physics of a particle in a magnetic field for decades; it's often considered textbook physics. However, scientists are still learning a lot about geometrical energy bands with additional potentials. In particular, this is a really new and important field in ultracold gases and photonics where there are many relevant recent experiments, all at the cutting-edge. We're talking to that community, and hopefully showing them that they will be able to study and understand much more than they might expect. We want to emphasize that there are lots of interesting connections with magnetism that can be revealed by studying the quantum physics of single particles.
"We are currently working on demonstrating how other experiments [besides realizing magnetism on a torus] would be able to study other analogue quantum magnetic phenomena in momentum space. There are many more possibilities still to be explored."
More information: Hannah M. Price, et al. "Quantum Mechanics with a Momentum-Space Artificial Magnetic Field." Physical Review Letters. DOI: 10.1103/PhysRevLett.113.190403
Journal information: Physical Review Letters
© 2014 Phys.org