October 2, 2014 feature
Superposition revisited: Proposed resolution of double-slit experiment paradox using Feynman path integral formalism
(Phys.org) —The Schrödinger's Cat thought experiment, published in 1926 by Erwin Schrödinger, may be the most widely-known metaphorical explanation of quantum superposition and collapse. (Superposition is a fundamental principle of quantum mechanics stating that a physical system – such as a photon or electron – simultaneously exists partly in all theoretically possible states; but when measured or observed gives a result corresponding to only one of the possible states.)
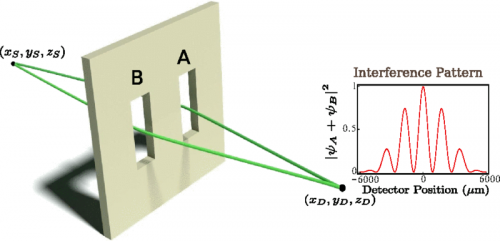
That being said, the earlier foundational double-slit experiment has the advantage of being, well, an actual experiment that provides a window into this often counterintuitive realm. (As a somewhat surprising aside, while the Michelson–Morley experiment, published in 1887 by Albert A. Michelson and Edward W. Morley, demonstrated temporal coherence, a much earlier device – Thomas Young's 1803 double-slit interferometer – demonstrated spatial coherence, contradicting Newtonian physics a century before quantum mechanics and special relativity by showing that light, like sound, was also a wave motion.) Despite its long legacy, however, the double-slit experiment remains the subject of research. One such focus is a curious discrepancy: The Schrödinger (yes, the same Schrödinger) equation, or wavefunction– which describes how the quantum state of a physical system changes with time – when both slits are open differs slightly from the sum of the wavefunctions with the two slits alternately open. The problem is that the three alternatives (slits A and B, slit A, slit B) correspond to separate boundary conditions – equations that specify the behavior of the solution to a system of differential equations at the boundary of that system's domain – meaning that superposition does not apply.
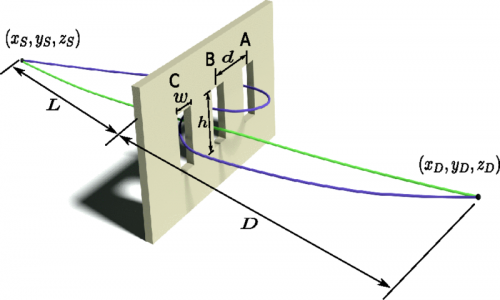
Recently, however, scientists at the Raman Research Institute and the Indian Institute of Science, both in Bangalore, India, theoretically resolved this paradox by quantifying nonclassical path contributions in quantum interference experiments using the Feynman path integral formalism, which involves an integration over all possible paths that can be taken by the particle through the two slits, thereby calculating a quantum amplitude by replacing the classical notion of a single, unique trajectory for a system with a sum, or functional integral, over an infinite number of possible trajectories. This allows them to replace the approximate wavefunction with both slits open (ψAB = ψA + ψB) with an integral that includes both the classical paths – the nearly straight paths from the source to the detector through either slit – and the nonclassical, or looped, paths that make a small but finite contribution to the total intensity at the detector screen (ψAB = ψA + ψB + ψL).
In so doing, they successfully quantified the effect of such nonclassical paths in interference experiments, which in turn quantifies the deviation from the common but incorrect application of the superposition principle in different possible experimental conditions. Although the researchers acknowledge that it would be difficult to create a direct experimental demonstration of the existence of these nonclassical paths, they conclude that since contributions from such paths can be significant. They therefore propose simple three-slit interference experiments to directly confirm their existence.
Prof. Urbasi Sinha, Raman Research Institute and Prof. Aninda Sinha, Indian Institute of Science discussed the paper that they and their co-authors published in Physical Review Letters. One of their main challenges was at the heart of their research: using the Feynman path integral formalism to quantify contributions from nonclassical paths to provide a measurable deviation from naive applications of the superposition principle. "In order to isolate the effect of the nonclassical paths we used the Sorkin parameter as proposed by Rafael D. Sorkin1," Aninda tells Phys.org. "Originally this parameter was proposed to test the Born rule, but it turned out to be a useful way to isolate the contribution of the curved paths." The Born rule (published by Max Born in his 1926 paper2) is a law of quantum mechanics which gives the probability that a measurement on a quantum system will yield a given result. "In addition, an earlier classical simulation of the Maxwell's equations3 led us into thinking about the problem in the realm of quantum mechanics."
Of equal import to the scientists – and a challenge that lies ahead of them, as well as to those researchers who respond to their proposal – is presenting a direct experimental demonstration for the existence of these nonclassical paths. "The nonclassical paths have always existed – the path integral formalism requires one to take into account the contribution from all possible paths," Urbasi explains. "However, these paths always tend to have contributions secondary to those from the classically dominant paths that extremize the action." This occurs in accordance with the action principle, which states that a particular functional of all paths that a particle can take between two points is extremized along the correct classical solution. "Thus, in spite of being present, the contribution to a certain propagator tends to be much smaller than the one from the classically dominant ones," Urbasi adds.
"This is what makes an experimental demonstration challenging," Urbasi continues, "since it requires a signal-to-noise ratio high enough to enable a non-zero measurement of a parameter known as kappa (κ) – the normalized version of the Sorkin parameter – as a function of detector position. Having said that, the path integral formalism enabled us to use the kappa symmetry to our advantage: Because it ensures that it is non-zero only in the presence of nonclassical paths, and zero otherwise, it provides a precise and convincing demonstration of the presence of these nonclassical paths."
Moving forward, Urbasi notes that using nonclassical path effects to model possible decoherence mechanisms in interferometer-based quantum computing applications is a direction the scientists wish to investigate in the near future. "Any quantum simulation which appeals to the phenomenon of interference should benefit from our approach – and regarding quantum computing itself, an interferometer-based quantum computing architecture immediately comes to mind. Our work highlights and suggests an experimental proposal to quantify non classical paths in interference experiments and hence comments on the commonly used naive application of the superposition principle in interference experiments. If a successful experiment is performed, then that will prove our assertions. Completing the picture in so far as application of the superposition principle in interference phenomena is concerned should definitely have ramifications in situations where interference is used as a resource."
Other areas of research will benefit from their study, Urbasi says, because their work gives them a more complete understanding of slit-based interference. "Richard Feynman famously said that 'the double-slit experiment has in it the heart of quantum mechanics. In reality, it contains the only mystery.4' Therefore, a more complete understanding there will be useful in all areas where interference is considered a resource. These include interferometer-based quantum computing protocols as well as observational radio astronomy data related to the early universe. In fact," Aninda points out, referring to the potential role of Feynman's path integral formalism and thereby looped nonclassical paths in the effort to construct a unified theory of quantum gravity, "there have been recent proposals in the cosmology literature which deal with a potential modification to the Born rule. For such modifications to be experimentally testable one will need precision calculation such as ours."
More information: Nonclassical Paths in Quantum Interference Experiments, Physical Review Letters 113, 120406: Published 19 September 2014, doi:10.1103/PhysRevLett.113.120406
Related:
1Quantum Mechanics As Quantum Measure Theory, Modern Physics Letters A 09, 3119 (1994), doi:10.1142/S021773239400294X (Earlier PDF version: arXiv:gr-qc/9401003v2)
2Zur Quantenmechanik der Stoßvorgänge, Max Born, Zeitschrift für Physik, 37, #12 (Dec. 1926), pp. 863–867 (German); English translation, On the quantum mechanics of collisions, in Quantum theory and measurement, Section I.2, J. A. Wheeler and W. H. Zurek, eds., Princeton, New Jersey: Princeton University Press (Paperback Edition, July 14, 2014), ISBN-13: 978-0691613161
3Analysis of multipath interference in three-slit experiments, Physical Review A 85, 012101 (4 January 2012), doi:10.1103/PhysRevA.85.012101
4The Feynman Lectures on Physics, Vol. I: The New Millennium Edition: Mainly Mechanics, Radiation, and Heat (October 4, 2011), Chapter 37 (Quantum Behavior), page 37-2 (An experiment with bullets). Paperback ISBN-13: 978-0465024933 | Online
Journal information: Physical Review Letters , Physical Review A
© 2014 Phys.org