Improvements to classical graph theory have potential to impact modern-day problem solving
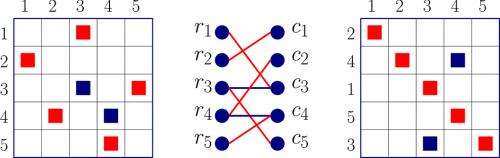
In a reexamination of existing combinatorial optimization (graph) algorithms used to find the best solution with minimum enumeration, scientists from Simula Research Laboratory (Norway), University of Bergen (Norway), Purdue University, and Pacific Northwest National Laboratory explored the maximum bipartite matching problem. In the context of solving a system of linear equations, this problem resolves how to obtain the maximum number of nonzeros on the diagonal of a sparse matrix, where most entries are zero, by exchanging rows and columns of the original matrix (refer to Figure 1), which can improve runtimes, efficiency, and minimize errors.
Their first-of-its-kind work involved exploiting modern multi-core computers, an area not previously explored for this algorithm, and provided a new parallel version of the push-relabel algorithm for bipartite graph matching that works well for shared memory computing systems. Their work also included a thorough examination of the algorithmic performance, showing viable and improved scaling on various multi-core machines.
Beyond the din of modern society's organized chaos—some obvious: thousands of airplanes zigzagging overhead at any given time; some not-so-obvious: exabytes of data traversing the Internet—it is easy to forget that the fuel underlying this progress and ingenuity is not unleaded. Instead, algorithms enable efficient execution of these activities—and many more. While the theoretical foundations for network flow and maximum matching were built as early as the 1950s by pioneers such as Ford, Fulkerson, Edmonds, Gale, and Shapley, the fundamental shift in computing warrants a reconsideration of these classical algorithms to exploit the power and efficiency of modern computers.
"Two things have happened in the recent past: our computers have become slower and parallel, and our data have grown several orders of magnitude," said Mahantesh Halappanavar, a scientist with PNNL's Data Sciences group (Analysis and Algorithms) and co-author of the paper describing this work. "Combinatorial algorithms are ubiquitous and help us solve many challenging problems not only in science, but in day-to-day life. Fast algorithms and efficient implementations targeting modern architectures and large-scale data will have wide and lasting impacts on numerous applications.
"However, as we discuss in the paper, parallelization is a challenging research problem with no easy solutions," he added. "Hence, we are exploring a new class of algorithms for maximum matching that have direct implication for other algorithms, such as network flows."
In their work, the researchers explored several techniques to expedite the computation of maximum matching, including using greedy initialization algorithms, search-space pruning techniques, and switching to serial computation when the algorithm runs out of concurrency. The impact of each technique was systematically studied and supported with experiments on a large set of input data chosen from a diverse set of applications. They then compared their new method with a separate class of algorithms based on the standard technique of augmentation. Some of the authors were previously involved in a detailed study regarding the efficiency of augmentation-based algorithms for maximum matching (refer to Azad et al. 2012). Employing a Cray XMT supercomputer, the researchers implemented all of the algorithms in the C/C++ programming language using the OpenMP programming model to exploit multi-core architectures. Experiments were conducted on multiple test systems with a varied numbers of processors to examine the scalability of the proposed algorithms and present several lessons that are important to other researchers.
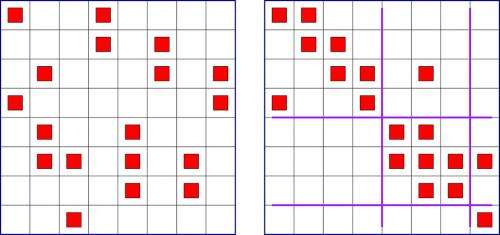
The techniques devised for the parallel push-relabel algorithms potentially could be expanded to preflow-push algorithms used for computing maximum flows. Typically, these algorithms are employed in transportation modeling or for examining human circulatory systems, atmospheric systems, or electrical current flows. Another immediate goal is to implement a complete pipeline for computing the block triangular form of a matrix (see Figure 2).
More information: Langguth J, A Azad, M Halappanavar, and F Manne. 2014. "On parallel push–relabel based algorithms for bipartite maximum matching." Parallel Computing 40(7):289-308. DOI: 10.1016/j.parco.2014.03.004.
Azad MA, M Halappanavar, S Rajamanickam, EG Boman, A Khan, and A Pothen. 2012. "Multithreaded Algorithms for Maximum Matching in Bipartite Graphs." In IEEE 26th International Parallel & Distributed Processing Symposium (IPDPS 2012), pp. 860-872. May 12-25, 2012, Shanghai, China. IEEE Computer Society, Los Alamitos, California. DOI: 10.1109/IPDPS.2012.82.
Provided by Pacific Northwest National Laboratory