Physicists provide experimental proof of theorized Efimov states
Some years ago, Rudolf Grimm's team of quantum physicists in Innsbruck provided experimental proof of Efimov states – a phenomenon that until then had been known only in theory. Now they have also measured the second Efimov resonance of three particles in an ultracold quantum gas, thus, proving the periodicity of this universal physical phenomenon experimentally.
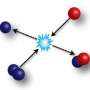
Eight years ago Rudolf Grimm's research group was the first to observe an Efimov state in an ultracold quantum gas. The Russian physicist Vitali Efimov theoretically predicted this exotic bound state of three particles in the 1970s. He forecast that three particles would form a bound state due to their quantum mechanical properties, under conditions when a two-body bound state would be absent. What is even more astounding: When the distance between the particles is increased by factor 22.7, another Efimov state appears, leading to an infinite series of these states. Until now this essential ingredient of the famous scenario has remained elusive and experimentally proving the periodicity of the famous scenario has presented a challenge. "There have been some indications that particles continuously create three-body states if the distance is increased by this factor," says Rudolf Grimm from the Institute of Experimental Physics of the University of Innsbruck and the Institute of Quantum Physics and Quantum Optics of the Austrian Academy of Sciences. "Proving the scenario was very difficult but we have finally been successful."
Bound in great distance
Ultracold quantum gases are highly suited for studying and observing quantum phenomena of particle systems experimentally as the interaction between atoms are well tunable by a magnetic field. However, Rudolf Grimm's research group got very close to the limits of what is possible experimentally when they had to increase the distance between the particles to one micrometer to be able to observe the second Efimov state. "This corresponds to 20,000 times the radius of a hydrogen atom," explains Grimm. "Compared to a molecule, this is a gigantic structure." This meant that the physicists had to be particularly precise with their work. What greatly helped the researchers in Innsbruck was their extensive experience with ultracold quantum gases and their great technical expertise. Their final result shows that the second Efimov state is larger than the first one by a factor of 21.0 with a measurement uncertainty of 1.3. "This small deviation from the factor 22.7 may be attributed to the physics beyond the ideal Efimov state, which is also an exciting topic," explains Rudolf Grimm.

New research area
The scientific community's interest in this phenomenon lies in its universal character. The law is equally applicable to nuclear physics, where strong interaction is responsible for the binding of particles in the atomic nucleus, and to molecular interactions that are based on electromagnetic forces. "Interaction between two particles and between many particles is well studied," says Grimm. "But we still need to investigate and learn about phenomena that arise from the interaction between only a few particles. The Efimov states are the basic example for this." The joint work of Rudolf Grimm's team and the British theoretical physicist Jeremy M. Hutson has been supported by the Austrian Science Fund. The results are now published in the journal Physical Review Letters.
More information: "Observation of the Second Triatomic Resonance in Efimov's Scenario." Bo Huang, Leonid A. Sidorenkov, Rudolf Grimm, Jeremy M. Hutson. Phys. Rev. Lett. 112, 190401 (2014) dx.doi.org/10.1103/PhysRevLett.112.190401, arXiv: arxiv.org/abs/1402.6161
Journal information: Physical Review Letters
Provided by University of Innsbruck