On the origins of the Schrodinger equation

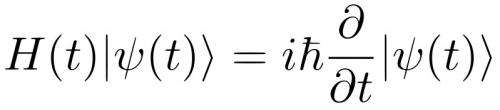
(Phys.org) —One of the cornerstones of quantum physics is the Schrödinger equation, which describes what a system of quantum objects such as atoms and subatomic particles will do in the future based on its current state. The classical analogies are Newton's second law and Hamiltonian mechanics, which predict what a classical system will do in the future given its current configuration. Although the Schrödinger equation was published in 1926, the authors of a new study explain that the equation's origins are still not fully appreciated by many physicists.

In a new paper published in PNAS, Wolfgang P. Schleich, et al., from institutions in Germany and the US, explain that physicists usually reach the Schrödinger equation using a mathematical recipe. In the new study, the scientists have shown that it's possible to obtain the Schrödinger equation from a simple mathematical identity, and found that the mathematics involved may help answer some of the fundamental questions regarding this important equation.

Although much of the paper involves complex mathematical equations, the physicists describe the question of the Schrödinger equation's origins in a poetic way:

"The birth of the time-dependent Schrödinger equation was perhaps not unlike the birth of a river. Often, it is difficult to locate uniquely its spring despite the fact that signs may officially mark its beginning. Usually, many bubbling brooks and streams merge suddenly to form a mighty river. In the case of quantum mechanics, there are so many convincing experimental results that many of the major textbooks do not really motivate the subject [of the Schrödinger equation's origins]. Instead, they often simply postulate the classical-to-quantum rules….The reason given is that 'it works.'"

Coauthor Marlan O. Scully, a physics professor at Texas A&M University, explains how physicists may use the Schrödinger equation throughout their careers, but many still lack a deeper understanding of the equation.

"Many physicists, maybe even most physicists, do not even think about the origins of the Schrödinger equation in the same sense that Schrödinger did," Scully told Phys.org. "We are often taught (see, for example, the classic book by Leonard Schiff, 'Quantum Mechanics') that energy is to be replaced by a time derivative and that momentum is to be replaced by a spatial derivative. And if you put this into a Hamiltonian for the classical dynamics of particles, you get the Schrödinger equation. It's too bad that we don't spend more time motivating and teaching a little bit of history to our students; but we don't and, as a consequence, many students don't know about the origins."

Scully added that understanding the history of both the science and the scientists involved can help in providing a deeper appreciation of the subject. In this way, the authors of the current paper are building on Schrödinger's own revolutionary discovery.

"Schrödinger was breaking new ground and did the heroic job of getting the right equation," Scully said. "How you get the right equation, is less important than getting it. He did such a wonderful job of then deriving the hydrogen atom wave function and much more. So did he understand what he had? You bet, he was really right on target. What we are trying to do is to understand more deeply the connection between classical and quantum mechanics by looking at things from different points of view, getting his result in different ways."

As the river analogy implies, there are many different ways to obtain the Schrödinger equation, with the most prominent one having been developed by Richard Feynman in 1948. But none of these approaches provides a satisfying explanation for one of the defining features of quantum mechanics: its linearity. Unlike the classical equations, which are nonlinear, the Schrödinger equation is linear. This linearity gives quantum mechanics some of its uniquely non-classical characteristics, such as the superposition of states.

In their paper, the physicists developed a new way to obtain the Schrödinger equation starting from a mathematical identity using classical statistical mechanics based on the Hamilton-Jacobi equation. To make the transition from the nonlinear classical wave equation to the linear Schrödinger equation—that is, from classical to quantum physics—the physicists made a few different choices regarding the amplitude of the wave and thereby linearized the nonlinear equation. Some of the choices resulted in a stronger coupling between the wave's amplitude and phase in comparison with the coupling in the classical equation.

"We have shown in a mathematical identity—the starting point of everything—that the choice of the coupling determines the nonlinearity or the linearity of the equation," Schleich, a physics professor at the University of Ulm, said. "In some wave equations, there is coupling between the amplitude and phase so that the phase determines the amplitude, but the amplitude does not determine the phase. In quantum mechanics, both amplitude and phase depend on each other, and this makes the quantum wave equation linear."

Because this coupling between amplitude and phase ensures the linearity of the equation, it is essentially what defines a quantum wave; for classical waves, the phase determines the amplitude but not vice versa, and so the wave equation is nonlinear.

"As we show in our paper, the Hamilton-Jacobi plus continuity logic leads to an equation which is very similar to the Schrödinger equation," Scully said. "But it's different and this difference is something that we consider important to understand. From one point of view, the extra term that comes into the nonlinear wave equation corresponding to classical physics (as opposed to the linear Schrödinger equation) shows that the classical equation is not linear and we cannot have superpositions of states. For example, we can't have right and left running waves adding to get standing waves because of this nonlinear term. It's when we have standing waves (left and right running wave solutions) that we most naturally get the eigenvalue solutions which we must, like the hydrogen atom eigenstates. So emphasizing linearity is very important."

The analysis also sheds some light on another old question regarding the Schrödinger equation, which is why does it involve an imaginary unit? In the past, physicists have debated whether the imaginary unit—which does not appear in classical equations—is a characteristic feature of quantum mechanics or whether it serves another purpose.

The results here suggest that the imaginary unit is not a characteristic quantum feature but is just a useful tool for combining two real equations into a single complex equation.

In the future, the physicists plan to extend their approach—which currently addresses single particles—to the phenomenon of entanglement, which involves multiple particles. They note that Schrödinger called entanglement the trait of quantum mechanics, and a better understanding of its origins could also reveal some interesting insight into the workings of the tiniest components of our world.

"We are presently looking at the problems from the point of view of current—how and to what extent can we regain quantum mechanics by relaxing the classical current idea and focus instead on a quantum-type current," Scully said. "From this perspective, we get into gauge invariance. There are lots of fun things that one can consider and we are trying to fit these together and see where each of these perspectives takes us. It is also fun to find out who has had ideas like this in the past and how all the ideas fit together to give us a deeper understanding of quantum mechanics. If our paper stimulates interest in this problem, it will have served its purpose."

Copyright 2013 Phys.org
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of Phys.org.