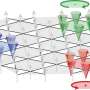
Explanation as to when a liquid on a rough surface will form a thin film and when it will form droplets

(Phys.org)—The phenomenon of liquids coating rough surfaces in the form of films or droplets is commonplace. The morning dew converts grass and leaves into scenes of magical beauty, while a thin film of rainwater on the road can pose a danger to every driver - especially if it freezes. But how can we tell in what conditions a liquid will form a continuous film or just isolated drops? Existing theories generally describe ideally smooth surfaces, which are not so relevant in the real world. Now, for the first time, scientists at the Max Planck Institute for Dynamics and Self-Organisation in Göttingen have developed a general theory that provides an answer to the question of film or droplets for rough surfaces. It is based on amazingly simple mathematical expressions - and could make it possible to predict, for instance, whether (and when) short circuits are likely to occur in transformer substations.
Liquids in large amounts are extraordinarily adaptable. They will fill any type of vessel and adapt their outer shape to any surface or border. Microscopically thin films of liquid, however, are a different story. They must mediate between the rough surface of an object and the free surface of the liquid, which always aims to be as smooth as possible due to the influence of surface tension. In this tightrope walk, less energy may be required to form tiny droplets on a surface than a film; this is the case of the morning dew that forms on leaves, spider webs and windscreens.
Now, for the first time, researchers from the Max Planck Institute for Dynamics and Self-Organisation in Göttingen have succeeded in establishing a general theory for this phenomenon, which is valid for the vast majority of natural surfaces. "Until now, physicists studying this issue have concentrated mainly on very special surfaces, such as those that have regular microscopic grooves", explains Stephan Herminghaus, Director at the Göttingen-based Institute. These can be produced by lithographic methods, among others, and are comparatively easy to describe in mathematical terms.
Vapour pressure and contact angle are the decisive factors
"The thing is, those ideal surfaces are nothing like the vast majority of surfaces we encounter in everyday life, from walls to tabletops", notes the physicist. Such 'everyday surfaces' are characterised by the irregular distribution of microscopic peaks and troughs that are subject to statistical fluctuations in terms of their size and shape. "In general, the dimensions of these structures range from many nanometres to a few micrometres", says Herminghaus.
In their calculations, the scientists in Göttingen describe this roughness as statistical height distribution, since the peaks and troughs occur in disordered arrangements. The only conditions are that the roughness is shallow, and similar over the whole surface. "This leads to amazingly simple expressions that require not more than school maths", explains Herminghaus. In his field of research, which routinely has recourse to complex computer simulations to solve difficult equations, this has created quite a stir.
The new equations reveal that the behaviour of liquids depends quite simply on two parameters: the contact angle, which gives the angle of the surface of the liquid against the substrate, and the vapour pressure in the surrounding air (i.e. the humidity). "On ideally smooth surfaces, vapour pressure is not so important", explains Herminghaus. There, the liquid does not have to adapt to so many margins and boundaries, such as those created by microscopic troughs and pits. On rough surfaces, however, its influence is considerable: just a small increase in pressure or angle can cause a film to suddenly transform into multiple droplets – or vice versa.
If the water pressure is too high, the lotus effect is lost
In these cases, physicists speak of a transition between two phases. In the wet phase, the liquid forms a practically continuous film over the rough surface. Almost all the microscopic troughs are filled, and only occasionally does a particularly high peak break the surface. In the dry phase, however, large portions of the surface remain untouched by the liquid, as it clumps together into droplets. "The system always selects the option that requires least energy in function of the vapour pressure and contact angle", says Herminghaus.
In principle, these new discoveries now allow the scientists to calculate what humidity value is required for a surface to be covered with a continuous film of liquid. In order to make this prognosis, they only need to know the statistical properties of the surface roughness. Such considerations could be of interest to the operators of transformer substations, for example, where short circuits can occur if a continuous film forms on the insulators. "As soon as they are worn rough by weathering, the ceramic surfaces used in the substations fulfil our conditions", explains Herminghaus. By contrast, the new findings are not yet suitable for predicting dampness in cellar walls. Some materials are simply too irregular, bricks being a case in point, with their coarse pores and sturdy structure. The theory will have to be extended before it can be applied to such materials.
The new discoveries are also relevant to the lotus effect, which makes liquids run off rough surfaces without sticking. The difference here is that a thin film of air assumes the role of the liquid, while the water plays the part of the air. When a film of air fills the troughs on the surface, drops of water cannot penetrate, but float on a kind of microscopic air cushion and run off. Only if the continuous film of air is broken, because the water pressure is too large, can the liquid penetrate the grooves and wet the surface of the leaf.
More information: Herminghaus, S. Universal Phase Diagram for Wetting on Mesoscale Roughness, Physical Review Letters, 109, 236102 (5 December 2012)
Journal information: Physical Review Letters
Provided by Max Planck Society