Chaotic 'spin vortices' could lead to new computer memories

(Phys.org)—In science, just like in life, sometimes creating the most effective organization depends on being able to handle just a bit of chaos first.

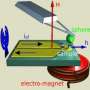
Scientists at the U.S. Department of Energy's Argonne National Laboratory have used alternating magnetic fields to control the behavior of "spin vortices" trapped in small dots made from iron and nickel that can be magnetized in two separate ways. While the majority of these structures are magnetized in-plane either clockwise or counter-clockwise, a tiny region at their centers – the vortex core – is magnetized out of plane, either up or down.

"If you were able to visualize it, it would look like a funnel," said Argonne materials scientist Valentyn Novosad.

Novosad and postdoctoral researcher Shikha Jain wanted to find a way to control the magnetic states of pairs or even large groups of these dots that interacted with each other in a lattice.

In the resting state, the cores of the dots are randomly polarized. After applying an oscillating magnetic field to the pairs of dots, the researchers observed that the central cores began to switch back and forth repeatedly between up- and down-magnetizations – which Jain and Novosad characterized as "chaos."

This chaotic system's behavior is dictated by the fact that the magnetic field, when applied, oscillates at a particular frequency that can be tuned to match the "resonance frequency" – that is, the natural frequency of vibration – for a specific polarity combination in a dot-pair. Each pair of dots has two resonance frequencies, corresponding to parallel (up-up or down-down) or antiparallel (up-down or down-up) magnetization states. In the parallel state, the dots' centers are magnetized in the same direction, while in the antiparallel state they are opposite.

By increasing and then decreasing the strength of the applied field, Argonne's scientists were able to bring the dots' magnetizations into and then out of chaos. When the amplitude of the oscillating field was reduced significantly, the researchers discovered that the new polarizations corresponded to the opposite state of the applied frequency. If the frequency corresponded to the parallel magnetization, an antiparallel arrangement would emerge, and vice versa.

"We were somewhat surprised that the behaviors of multiple dots could be controlled so precisely," Jain said. "There had been a lot of work done before on single-dot systems, but no one had really investigated how magnetic dots interact with each other in this kind of environment."

By achieving consistent control of the central polarization's direction, the researchers moved one step closer to creating new magnetic devices, including non-volatile random access memories. These devices are the subject of intense research in academia and industry worldwide as they offer energy efficiency, high operating speed and exceptional reliability. Unlike the silicon-based chips in today's computers, their magnetic counterparts employ spin rather than electric charge to store and process information.

According to Novosad, the underlying physics that governs the two-dot interaction should apply as well to a system of many elements. Future studies will seek to explore the collective dynamics in larger three-dimensional crystal-like magnetic structures.

These results were published in the journal Nature Communications. The paper is titled "From chaos to selective ordering of vortex cores in interacting mesomagnets."