July 23, 2012 feature
Can quantum theory be improved?
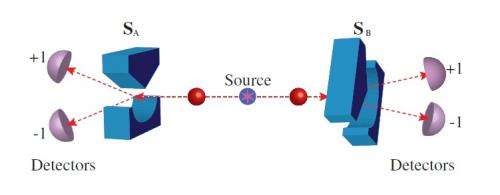
(Phys.org) -- Being correct 50% of the time when calling heads or tails on a coin toss won’t impress anyone. So when quantum theory predicts that an entangled particle will reach one of two detectors with just a 50% probability, many physicists have naturally sought better predictions. The predictive power of quantum theory is, in this case, equal to a random guess. Building on nearly a century of investigative work on this topic, a team of physicists has recently performed an experiment whose results show that, despite its imperfections, quantum theory still seems to be the optimal way to predict measurement outcomes.
The physicists, Terence E. Stuart, et al., from the University of Calgary in Alberta, Canada; ETH Zurich in Switzerland; and the Perimeter Institute for Theoretical Physics in Waterloo, Ontario, Canada, have published their paper on the predictive power of quantum theory and alternative theories in a recent issue of Physical Review Letters.
“The fact that certain outcomes can only be predicted with probability 50% by quantum theory could in principle be explained in two very different ways,” coauthor Renato Renner of ETH Zurich told Phys.org. “One would be that quantum theory is an incomplete theory whose predictions are only random because we have not yet discovered the parameters that are relevant for determining the outcomes (and that another yet-to-be-discovered theory would therefore allow for better predictions). The other explanation would be that there is ‘inherent’ randomness in Nature. Our work excludes the first possibility. In other words, it is not only quantum theory that predicts randomness, but there is ‘real’ randomness in Nature.”
The physicists began by asking whether it may be possible to improve quantum theory’s predictive power by supplementing it with some additional information (i.e., a local hidden variable). With complete information about a scenario, classical theories can predict an outcome with 100% accuracy. But in the 1960s, physicist John Bell proved that no local hidden variable exists that could enable quantum theory to predict an outcome with complete certainty.
However, Bell’s work didn’t rule out the possibility that quantum theory’s predictive power could be improved a little bit, nor did it refute the existence of any alternative probabilistic theory that has more predictive power than quantum theory.
One recent proposal for improving quantum mechanical prediction was suggested by physicist Tony Leggett in 2003. In this model, a hidden spin vector could increase the predictive probability of quantum theory by 0.25, from 0.5 to 0.75 (with 1.0 being complete certainty). Although Leggett showed that this model is incompatible with quantum theory, there has been no reason to assume that other models don’t exist.
However, in the new paper, the physicists have experimentally demonstrated that there cannot exist any alternative theory that increases the predictive probability of quantum theory by more than 0.165, with the only assumption being that measurement parameters can be chosen independently of the other parameters of the theory. In other words, any current or future theory that can improve upon quantum theory by more than 0.165 would either be falsified by the physicists’ experimental observations here (such as Leggett’s model) or be incompatible with the free choice assumption (one example being the de Broglie-Bohm theory).
As Renner explained, it is impossible to know exactly how many alternative theories there are because most are small variations of others. Some, such as the de Broglie-Bohm theory, date back to the early days of quantum theory while others were proposed more recently, partially motivated by information-theoretic considerations. He also added that giving up the free choice assumption has its own complications.
“Our work excludes any such theory,” he said. “But there is one way to circumvent this conclusion: One may give up the assumption of ‘free choice’ on which our result is based and replace it by a weaker notion. This is possible in principle, but would, for instance, necessarily lead to an incompatibility with relativistic space-time structure.”
The researchers’ experiments involved sending a pair of entangled photons through an apparatus and making measurements to determine whether they arrive at one of two detectors. By improving the fidelity of the photon pair sources and improving the quality of the measurement apparatuses, the scientists explain that the 0.165 bound they measured here could be improved. However, decreasing this bound by more than a factor of two would require improvements that are beyond current state-of-the-art technology.
Nevertheless, the experimental results provide the tightest constraints yet on alternatives to quantum theory. The findings imply that quantum theory is close to optimal in terms of its predictive power, even when the predictions are completely random. In the future, the physicists plan to further investigate the implications of these results.
“On the theory side, this work opens a number of interesting questions related to the nature of randomness,” Renner said. “One of them is whether randomness can be ‘amplified,’ i.e., whether there are processes that start with low-quality randomness and produce virtually perfect randomness.”
The scientists already have a first result in this direction, which was published earlier this year in Nature Physics.
More information: Terence E. Stuart, et al. “Experimental Bound on the Maximum Predictive Power of Physical Theories.” PRL 109, 020402 (2012). DOI: 10.1103/PhysRevLett.109.020402
Journal information: Physical Review Letters , Nature Physics
Copyright 2012 Phys.org
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.