Rice University physicists have created a tiny "electron superhighway" that could one day be useful for building a quantum computer, a new type of computer that will use quantum particles in place of the digital transistors found in today's microchips.
In a recent paper in Physical Review Letters, Rice physicists Rui-Rui Du and Ivan Knez describe a new method for making a tiny device called a "quantum spin Hall topological insulator." The device, which acts as an electron superhighway, is one of the building blocks needed to create quantum particles that store and manipulate data.
Today's computers use binary bits of data that are either ones or zeros. Quantum computers would use quantum bits, or "qubits," which can be both ones and zeros at the same time, thanks to the quirks of quantum mechanics.
This quirk gives quantum computers a huge edge in performing particular types of calculations, said Du, professor of physics and astronomy at Rice. For example, intense computing tasks like code-breaking, climate modeling and biomedical simulation could be completed thousands of times faster with quantum computers.
"In principle, we don't need many qubits to create a powerful computer," he said. "In terms of information density, a silicon microprocessor with 1 billion transistors would be roughly equal to a quantum processor with 30 qubits."
In the race to build quantum computers, researchers are taking a number of approaches to creating qubits. Regardless of the approach, a common problem is making certain that information encoded into qubits isn't lost over time due to quantum fluctuations. This is known as "fault tolerance."
The approach Du and Knez are following is called "topological quantum computing." Topological designs are expected to be more fault-tolerant than other types of quantum computers because each qubit in a topological quantum computer will be made from a pair of quantum particles that have a virtually immutable shared identity. The catch to the topological approach is that physicists have yet to create or observe one of these stable pairs of particles, which are called "Majorana fermions" (pronounced MAH-yor-ah-na FUR-mee-ons).
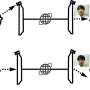
The elusive Majorana fermions were first proposed in 1937, although the race to create them in a chip has just begun. In particular, physicists believe the particles can be made by marrying a two-dimensional topological insulator -- like the one created by Du and Knez -- to a superconductor.
Topological insulators are oddities; although electricity cannot flow through them, it can flow around their narrow outer edges. If a small square of a topological insulator is attached to a superconductor, Knez said, the elusive Majorana fermions are expected to appear precisely where the materials meet. If this proves true, the devices could potentially be used to generate qubits for quantum computing, he said.
Knez spent more than a year refining the techniques to create Rice's topological insulator. The device is made from a commercial-grade semiconductor that's commonly used in making night-vision goggles. Du said it is the first 2-D topological insulator made from a material that physicists already know how to attach to a superconductor.
"We are well-positioned for the next step," Du said. "Meanwhile, only experiments can tell whether we can find Majorana fermions and whether they are good candidates for creating stable qubits."
Explore further:
A quantum simulator for magnetic materials
