Two new papers in the Journal of General Physiology demonstrate the successes of using bifurcation theory and dynamical systems approaches to solve biological puzzles.
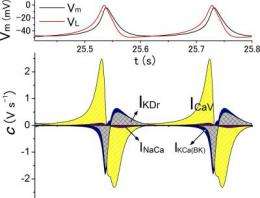
In companion papers, Akinori Noma and colleagues from Japan first present computer simulations of a model for bursting electrical activity in pancreatic beta cells, and then use bifurcation diagrams to analyze the behavior of the model. In his Commentary accompanying the articles, Arthur Sherman (National Institutes of Health) proposes that the methods demonstrated in these two papers have broader implications and demonstrate the increasingly important role of dynamical systems approaches in the field of biology.
Mathematical modeling is an important tool in understanding complex cellular processes. Unlike time-based simulations of models, which test only one set of parameter values, bifurcation diagrams analyze the solutions of the governing equations as a function of critical parameters. Such bifurcation scenarios are a powerful tool for dissecting complex systems by subdividing them into parameter regions that underlie distinct behavioral patterns, Sherman explains. He proposes that dynamic modeling will become a more prominently used tool for biologists as live cell–imaging techniques continue to reveal greater complexity and more cell-signaling mechanisms.
Explore further:
X-ray tomography on a living frog embryo
More information: The articles appear online on June 27 www.jgp.org
