Peregrine's 'Soliton' observed at last
(PhysOrg.com) -- An old mathematical solution proposed as a prototype of the infamous ocean rogue waves responsible for many maritime catastrophes has been observed in a continuous physical system for the first time.
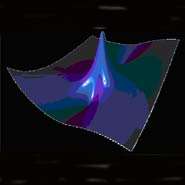
The Peregrine 'Soliton', discovered over 25 years ago by the late Howell Peregrine (1938-2007), an internationally renowned Professor of Applied Mathematics formerly based at the University of Bristol, is a localised solution to a complex partial differential equation known as the nonlinear Schrodinger equation (NLSE).
The Peregrine solution is of great physical significance because its intense localisation has led it to be proposed as a prototype of ocean rogue waves and also represents a special mathematical limit of a wide class of periodic solutions to the NLSE.
Yet despite its central place as a defining object of nonlinear science for over 25 years, the unique characteristics of this very special nonlinear wave have never been directly observed in a continuous physical system - until now.
An international research team from France, Ireland, Australia and Finland report the first observation of highly localised waves possessing near-ideal Peregrine soliton characteristics in the prestigious journal, Nature Physics.
The researchers carried out their experiments using light rather than water, but were are able to rigorously test Peregrine’s prediction by exploiting the mathematical equivalence between the propagation of nonlinear waves on water and the evolution of intense light pulses in optical fibres.
By building on decades of advanced development in fibre-optics and ultrafast optics instrumentation, the researchers were able to explicitly measure the ultrafast temporal properties of the generated soliton wave, and carefully compare their results with Peregrine’s prediction.
Their results represent the first direct measurements of Peregrine soliton localisation in a continuous wave environment in physics. In fact, the authors are careful to remark that a mathematically perfect Peregrine solution may never actually be observable in practice, but they also show that its intense localisation appears even under non-ideal excitation conditions.
This is an especially important result for understanding how high intensity rogue waves may form in the very noisy and imperfect environment of the open ocean.
The findings also highlight the important role that experiments from optics can play in clarifying ideas from other domains of science. In particular, since related dynamics governed by the same NLSE propagation model are also observed in many other systems such as plasmas and Bose Einstein Condensates, the results are expected to stimulate new research directions in many other fields.
---------
8/24/2010: This is a corrected version of the article.
More information: The paper is available to view via the following URL: dx.doi.org/10.1038/NPHYS1740
Provided by University of Bristol